Cho hình chữ nhật ABCD. Trên cạnh AB lấy M. Tìm vị trí của M để .
A. M là điểm thuộc đoạn AB sao cho AM = MB
B. M là điểm thuộc đoạn AB sao cho AM = MB
C. M là trung điểm đoạn AB
D. M là điểm thuộc đoạn AB sao cho AM = AB
 Giải bởi Vietjack
Giải bởi Vietjack
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hình chữ nhật có diện tích là 240, chiều rộng là 8cm. Chu vi hình chữ nhật đó là:
Cho hình chữ nhật ABCD có AD = 8cm, AB = 9cm. Các điểm M, N trên đường chéo BD sao cho BM = MN = ND. Tính diện tích tam giác CMN.
Tính diện tích của tam giác đều ABC biết chu vi tam giác ABC bằng 18cm.
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết OA = 12cm, diện tích hình thoi ABCD là 168. Cạnh của hình thoi là:
Cho hình thang ABCD, AB song song với CD, đường cao AH. Biết AB = 7cm; CD = 10cm, diện tích của ABCD là 25,5 thì độ dài AH là:
Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó. Chọn câu đúng.
Cho hình thang ABCD, đường cao ứng với cạnh DC là AH = 6cm; cạnh DC = 12cm. Diện tích của hình bình hành ABCD là:
Cho hình vuông MNPQ nội tiếp tam giác ABC vuông cân tại A (hình vẽ). Biết . Tính .
Một tam giác có độ dài ba cạnh là 12cm, 5cm, 13cm. Diện tích tam giác đó là
Hình chữ nhật có chiều dài tăng 4 lần, chiều rộng giảm 2 lần, khi đó diện tích hình chữ nhật
1. Khái niệm về đa giác
Định nghĩa: Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
• Đa giác ABCDE là hình gồm năm đoạn thẳng AB, BC, CD, DE, EA, trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng AB, BC, CD, DE, EA được gọi là các cạnh của đa giác đó.
Khi đó, đa giác ABCDE là đa giác lồi.
Chú ý: Từ nay nếu nhắc đến đa giác thì ta quy ước đó là đa giác lồi.
2. Đa giác đều
Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
3. Khái niệm diện tích đa giác
• Số đo của một phần mặt phẳng giới hạn bởi một đa giác được gọi là diện tích đa giác đó.
• Mỗi đa giác có một diện tích xác định. Diện tích đa giác là một số dương.
Diện tích đa giác có các tính chất sau:
• Hai tam giác bằng nhau thì có diện tích bằng nhau.
• Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích của những đa giác đó.
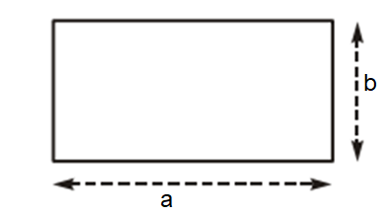
4. Công thức diện tích hình chữ nhật
Diện tích hình chữ nhật là tích hai kích thức của nó: S = a . b
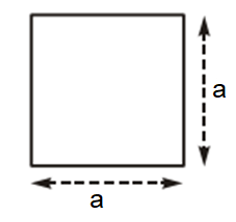
5. Công thức diện tích hình vuông, diện tích tam giác vuông
Diện tích hình vuông bằng bình phương cạnh của nó: S = .
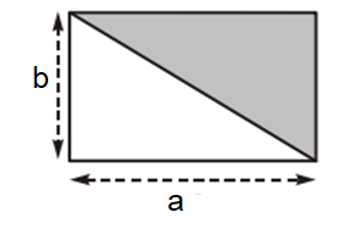
Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông: S = a.b.
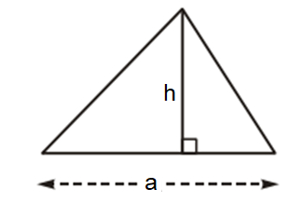
5. Công thức diện tích tam giác
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
S = a . h.
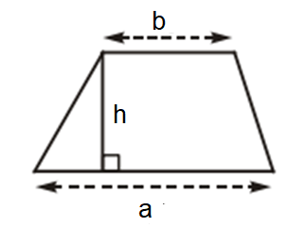
6. Công thức diện tích của hình thang
Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.
S = (a + b) . h
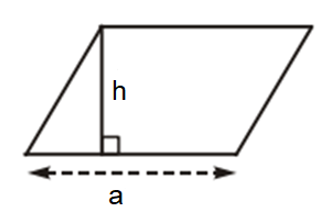
7. Công thức tính diện tích hình bình hành
Diện tích hình bình hành bằng tích của một cạnh với chiều cao tương ứng với cạnh đó: S = a . h
8. Diện tích tứ giác có hai đường chéo vuông góc
Diện tích của một tứ giác có hai đường chéo vuông góc bằng nửa tích độ dài hai đường chéo đó.
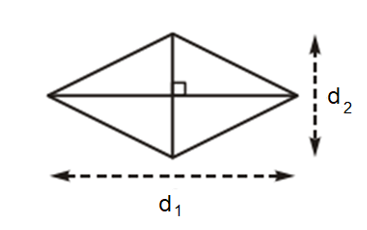
9. Công thức tính diện tích hình thoi
Diện tích hình thoi bằng nửa tích hai đường chéo.
S = d1 . d2
10. Cách tính diện tích đa giác
• Với một đa giác bất kì không có công thức tính. Cụ thể, ta có thể thực hiện các cách sau để tính diện tích đa giác:
+ Chia đa giác đó thành các tam giác riêng biệt rồi tính diện tích từng tam giác sau đó cộng các kết quả lại với nhau.
+ Tạo ra một tam giác chứa đa giác đó rồi tính diện tích đa giác bằng cách lấy tam giác lớn trừ đi diện tích của các “phần thừa”.
• Với một số hình đặc biệt ta có thể chia đa giác thành nhiều phần, mỗi phần đều là những hình mà ta dễ tính diện tích như: hình thang vuông, hình thoi, hình chữ nhật, hình vuông,...