Cho tam giác ABC, điểm M thuộc cạnh BC sao cho . Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 30cm. Chu vi của các tam giác DBM và EMC lần lượt là
A. 10cm; 15cm
B. 12cm; 16cm
C. 20cm; 10cm
D. 10cm; 20cm
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Ta có: MD // AC nên ΔDBM ~ ΔABC. Suy ra
Do đó
Chu vi ΔDBM bằng
Ta có ME // AB nên ΔEMC ~ ΔABC. Suy ra , do đó
Chu vi ΔEMC bằng cm
Vậy chu vi ΔDBM và chu vi ΔEMC lần lượt là 10cm; 20cm
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình bình hành ABCD. Trên đường chéo AC lấy điểm E sao cho AC = 3AE. Qua E vẽ đường thẳng song song với CD, cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau
(I) ΔAME ~ ΔADC, tỉ số đồng dạng
(II) ΔCBA ~ ΔADC, tỉ số đồng dạng bằng
(III) ΔCNE ~ ΔADC, tỉ số đồng dạng
Số khẳng định đúng là:
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho . Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Tỉ số chu vi hai tam giác ΔDBM và ΔEMC là
Cho hình bình hành ABCD. Trên đường chéo AC lấy điểm E sao cho AC = 3AE. Qua E vẽ đường thẳng song song với CD, cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau
(I) ΔAME ~ ΔADC, tỉ số đồng dạng
(II) ΔCBA ~ ΔADC, tỉ số đồng dạng bằng
(III) ΔCNE ~ ΔADC, tỉ số đồng dạng
Chọn câu đúng.
1.Tam giác đồng dạng
a) Định nghĩa
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
và
Tam giác A’B’C’ đồng dạng với tam giác ABC được kí hiệu là ∆A’B’C’ ∆ ABC.
Tỉ số các cạnh tương ứng được gọi là tỉ số đồng dạng
b) Tính chất
Các tính chất của hai tam giác đồng dạng:
Tính chất 1. Mỗi tam giác đồng dạng với chính nó.
Tính chất 2. Nếu ∆ABC ∆ A’B’C’ thì ∆A’B’C’ ∆ ABC.
Tính chất 3. Nếu ∆A’B’C’ ∆ A”B”C” và ∆A”B”C” ∆ ABC thì ∆A’B’C’ ∆ ABC.
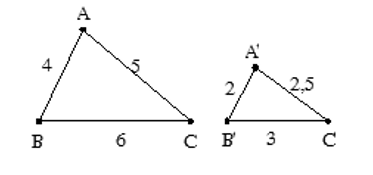
Ví dụ 1. Cho ∆A’B’C’ ∆ ABC như hình vẽ. Tính tỉ số đồng dạng ?
Lời giải:
Ta có ∆A’B’C’ ∆ ABC. Khi đó tỉ số đồng dạng là
2. Định lý
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
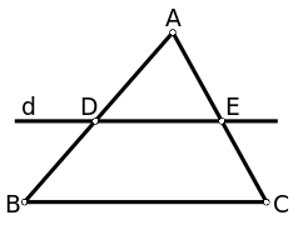

- Chú ý: Định lí cũng đúng cho trường hợp đường thẳng d cắt phần kéo dài của hai tam giác song song với cạnh còn lại.