Lựa chọn đáp án đúng nhất
Tìm câu trả lời sai
Cho △ABC vuông tại A có AC = 12BC, M là trung điểm của cạnh BC. Ta có:
A. MA = MB = MC
B.
C. đều
D. đều
 Giải bởi Vietjack
Giải bởi Vietjack

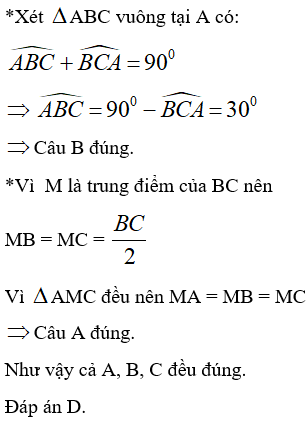
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Điền từ thích hợp vào chỗ trống
Cho tam giác ABC vuông cân tại A có O là trung điểm của cạnh BC.
Qua O kẻ đường thẳng d bất kỳ không qua đỉnh của tam giác. Kẻ BI, AH, CK vuông góc với d.
Tính , biết rằng BC = 10cm.
Đáp án: ___(cm)
Nối từ hoặc cụm từ ở cột bên trái với cột bên phải để được câu hoàn chỉnh
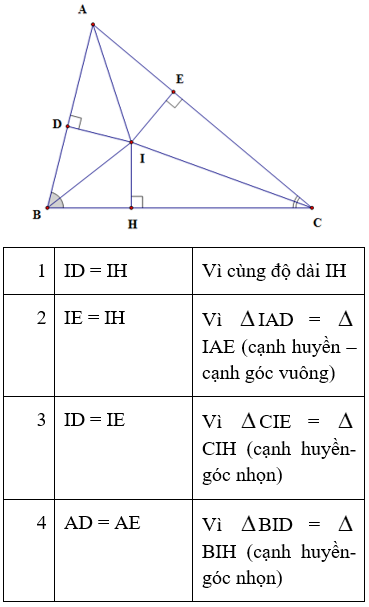
(Cho △ABC. Các tia phân giác của góc B và C cắt nhau ở I.
Kẻ ID ⊥ AB( D ∈ AB),IE ⊥ AC(E ∈ AC),IH ⊥ AB(H ∈ AB). Khi đó:
Lựa chọn đúng hay sai
(Lựa chọn đúng hay sai)
Cho ΔABC cân tại A. Kẻ CH ⊥ AB(H ∈ AB). Kẻ đường thẳng d qua C vuông góc với AC. Kẻ BK ⊥ d(K ∈ d). Khi đó:
|
|
Đúng |
Sai |
|
BK // AC |
|
|
|
|
|
|
|
BHC = BKC |
|
|
|
CK = CH |
|
|
Lựa chọn đáp án đúng nhất
Phát biểu sau ''Đúng'' hay ''Sai''
''Trong một tam giác cân, đường phân giác của góc ở đỉnh là đường cao ứng với đáy của tam giác đó''
Lựa chọn đúng hay sai
Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt đường trung trực của BC tại I. Qua I kẻ đường thẳng vuông góc với hai cạnh của góc A, cắt các tia AB, AC theo thứ tự tại H và K. Khi đó:
1. AH = AK
2. BH = CK
3.
4.
Lựa chọn đáp án đúng nhất
Cho tam giác cân ABC (AB = AC).D là một điểm trên AB, E là một điểm trên AC sao cho AD = AE. Từ D và E hạ các đường DM và EN cùng vuông góc với đáy BC. Khi đó:
Lựa chọn đúng hay sai
(Lựa chọn đúng hay sai)
Cho tam giác ABC cân tại A có . Kẻ BD ⊥ AC tại D, kẻ CE ⊥ AB tại E.
Gọi K là giao điểm của của BD và CE, I là trung điểm của BC. Khi đó:
1. BCE = CBD
2. BEK = CDK
3. AK là tia phân giác của
4. Ba điểm A, K, I thẳng hàng
Lựa chọn đúng hay sai
Cho tam giác ABC vuông cân tại A, N là trung điểm của BC, lấy điểm I nằm giữa N và C. Kẻ BE và CH cùng vuông góc với đường thẳng AI (E và H thuộc đường thẳng AI). Khi đó:
|
|
Đúng |
Sai |
|
BE = AH |
|
|
|
NAE = NCH |
|
|
|
|
|
|
|
NEH vuông cân tại H |
|
|
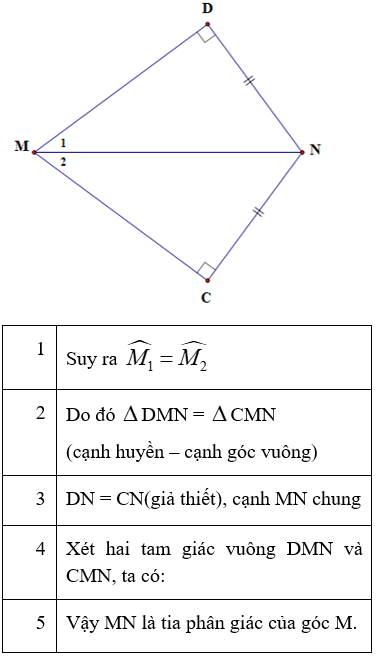
Sắp xếp các câu
(Hãy sắp xếp các ý chứng minh MN là tia phân giác của góc M.)