Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD.
1. Tính độ dài các đoạn AD, DC lần lượt là
A. 6cm, 4cm
B. 2cm, 5cm
C. 5cm, 3cm
D. 3cm, 5cm
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
+ Áp dụng định lý Pitago trong tam giác vuông ABC ta có:
+ Vì BD là đường phân giác của tam giác ABC nên áp dụng tính chất đường phân giác của tam giác, ta có:
=> AD = 3cm => DC = AC - AD = 8 - 3 = 5cm
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC, phân giác AD. Gọi E, F lần lượt là hình chiếu của B và C lên AD. Chọn khẳng định không đúng.
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD.
2. Chọn khẳng định đúng.
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,5cm và HC = 9cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.
Cho tam giác ABC, phân giác AD. Gọi E, F lần lượt là hình chiếu của B và C lên AD. Chọn khẳng định đúng.
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh BC thành hai đoạn thẳng HB = 7cm và HC = 18cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD. Gọi I là giao điểm của AH và BD.
1. Chọn kết luận đúng.
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm, đường cao AH, đường phân giác BD.
2. Gọi I là giao điểm của AH và BD. Chọn câu đúng.
1. Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông
Hai tam giác vuông đồng dạng với nhau nếu:
+ Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.
+ Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.
2. Dấu hiệu đặc biệt nhận biết hai tam vuông đồng dạng
- Định lý 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
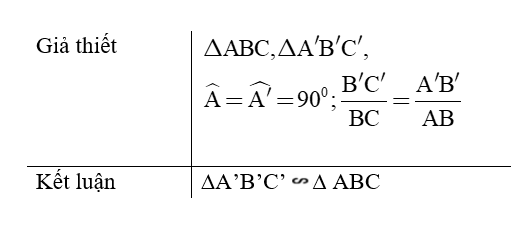
3. Tỉ số hai đường cao, tỉ số diện tích của hai tam giác đồng dạng
- Định lý 2: Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
Cho hai tam giác ABC và A’B’C’ với tỉ số đồng dạng là , hai đường cao tương ứng là AH và A’H’.
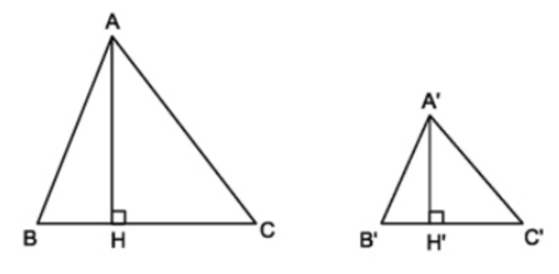
Khi đó, ta có tỉ số hai đường cao là : .
- Định lý 3: Tỉ số diện tích hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.

Ví dụ 1. Cho tam giác ABC đồng dạng với tam giác MNP theo tỉ số . Biết đường cao xuất phát từ A của tam giác ABC là AH = 12cm. Tính đường cao xuất phát từ M của tam giác MNP?
Lời giải:
Gọi đường cao xuất phát từ M của tam giác MNP là MK.
Vì tam giác ABC đồng dạng với tam giác MNP theo tỉ số nên