Cho hình chữ nhật ABCD có E là trung điểm của AB. Tia DE cắt AC ở F, cắt CB ở G. Chọn câu đúng.

1. Định lí Ta- let trong tam giác

1.1. Tỉ số của hai đường thẳng

- Định nghĩa

Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là $\frac{AB}{CD}$.

- Chú ý: Tỉ số của hai đoạn thẳng không phụ thuộc vào cách chọn đơn vị đo

Ví dụ 1.

- Cho  AB = 10 cm; CD = 30 cm thì $\frac{AB}{CD}=\frac{10}{30}=\frac{1}{3}.$

- Cho AB = 1 dm; CD = 3 dm thì $\frac{AB}{CD}=\frac{1}{3}.$

1.2. Đoạn thẳng tỉ lệ

- Định nghĩa:

Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức $\frac{AB}{CD}=\frac{A^{\text{'}}{B}^{\text{'}}}{C^{\text{'}}{D}^{\text{'}}}$ hay $\frac{AB}{A^{\text{'}}{B}^{\text{'}}}=\frac{CD}{C^{\text{'}}{D}^{\text{'}}}$ .

1.3. Định lý Ta – lét trong tam giác

- Định lý Ta – lét:

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lai thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.

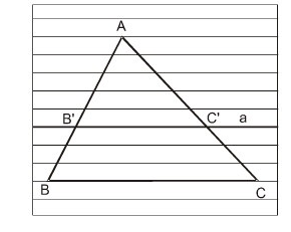
Tổng quát :$\Delta ABC,B^{\text{'}}{C}^{\text{'}}//BC;B^{\text{'}}\in AB,C^{\text{'}}\in AC$

Ta có:$\frac{A{B}^{\text{'}}}{AB}=\frac{A{C}^{\text{'}}}{AC};\frac{A{B}^{\text{'}}}{B{B}^{\text{'}}}=\frac{A{C}^{\text{'}}}{C^{\text{'}}C};\frac{B{B}^{\text{'}}}{AB}=\frac{C{C}^{\text{'}}}{AC}$

Ví dụ 2. Tính độ dài cạnh AN trong hình vẽ sau, biết MN// BC

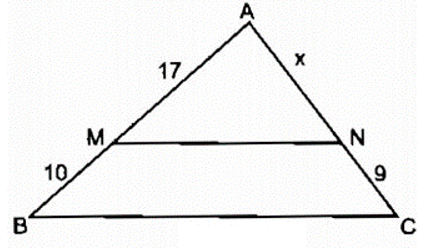
Lời giải:

Ta có MN// BC, áp dụng định lý Ta – lét ta có:

 $\frac{AM}{MB}=\frac{AN}{NC}$ hay $\frac{17}{10}=\frac{x}{9}$

$\Rightarrow x=\frac{17.9}{10}=15,3$

Vậy AN = 15,3.

2. Định lí đảo và hệ quả của định lí Ta – lét

2.1. Định lý đảo

- Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

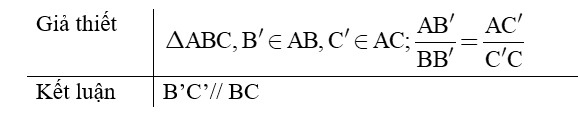
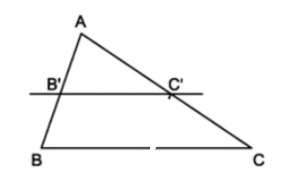
Ví dụ 3. Trong tam giác ABC có AB = 10cm; AC = 15cm. Lấy trên cạnh AB điểm B’, trên cạnh AC lấy điểm  C’ sao cho AB’ = 4cm; AC’ = 6cm. Chứng minh B’C’// BC.

Lời giải:

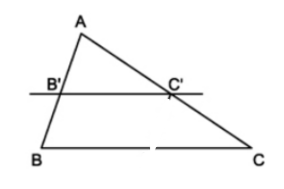
Ta có: B’B = AB – AB’ = 10 – 4 = 6cm,

Và CC’ = AC – AC’ = 15 – 6 = 9 cm

Ta có:

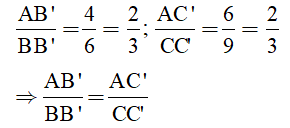
Theo định lí ta – lét đảo, suy ra: B’C’ // BC.

2.2. Hệ quả của định lý Ta – lét

- Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.

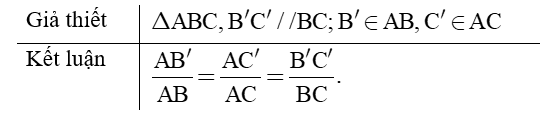
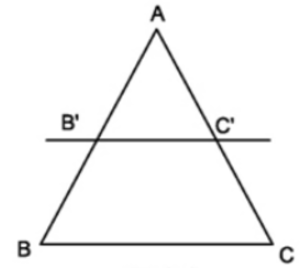
- Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng song song với một cạnh và cắt phần kéo dài của hai cạnh còn lại.

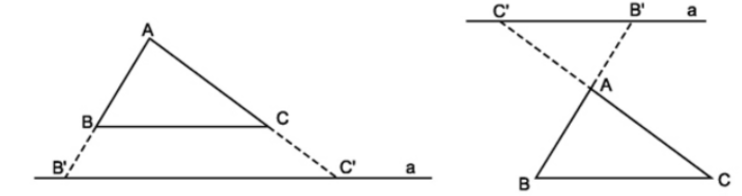
Ví dụ 4. Trong tam giác ABC có AB = 6cm và B’C’// BC . Lấy trên cạnh AB điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4cm; AC’ = 3cm. Tính độ dài cạnh AC.

Lời giải:

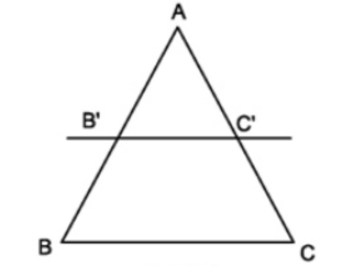
Áp dụng hệ quả trên ta có:

$\frac{A{B}^{\text{'}}}{AB}=\frac{A{C}^{\text{'}}}{AC}=\frac{B^{\text{'}}{C}^{\text{'}}}{BC}.$

Khi đó ta có:

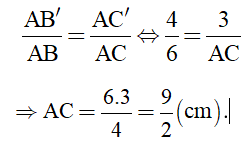
3. Tính chất đường phân giác của tam giác

3.1. Định lý

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.

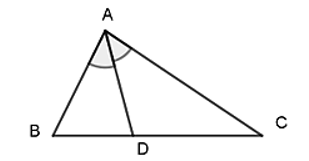
Ví dụ 5. Cho tam giác ABC có AD là đường phân giác của góc  $\widehat{BAC}$ sao cho DB = 4cm, AB = 6cm; AC = 8cm. Tính độ dài cạnh DC.

Lời giải:

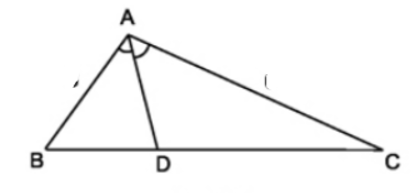
Áp dụng định lí trên ta có:

$\frac{DB}{DC}=\frac{AB}{AC}$

Hay $\frac{4}{DC}=\frac{6}{8}\Rightarrow DC=\frac{4.8}{6}=\frac{16}{3}cm$

3.2. Chú ý

Định lí vẫn đúng với đường phân giác của góc ngoài của tam giác

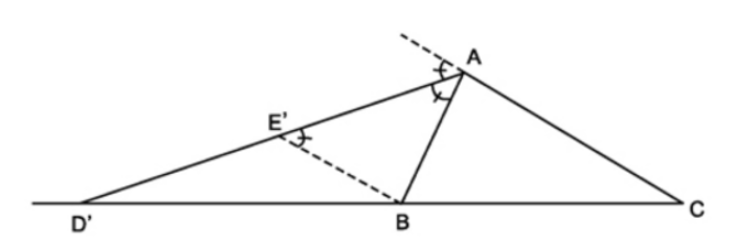
Nếu AE’ là phân giác của góc $\widehat{BAx}$

Ta có: $\frac{AB}{AC}=\frac{D\text{'}B}{D\text{'}C}$ .

4. Khái niệm tam giác đồng dạng

4.1.Tam giác đồng dạng

a) Định nghĩa

Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:

$\widehat{A}=\widehat{A^{\text{'}}};\widehat{B}=\widehat{B^{\text{'}}};\widehat{C}=\widehat{C^{\text{'}}}$ và $\frac{A^{\text{'}}{B}^{\text{'}}}{AB}=\frac{A^{\text{'}}{C}^{\text{'}}}{AC}=\frac{B^{\text{'}}{C}^{\text{'}}}{BC}$

Tam giác A’B’C’ đồng dạng với tam giác ABC được kí hiệu là ∆A’B’C’ $~$∆ ABC.

Tỉ số các cạnh tương ứng $\frac{A^{\text{'}}{B}^{\text{'}}}{AB}=\frac{A^{\text{'}}{C}^{\text{'}}}{AC}=\frac{B^{\text{'}}{C}^{\text{'}}}{BC}=k$  được gọi là tỉ số đồng dạng

b) Tính chất

Các tính chất của hai tam giác đồng dạng:

Tính chất 1. Mỗi tam giác đồng dạng với chính nó.

Tính chất 2. Nếu  ∆ABC$~$ ∆ A’B’C’   thì  ∆A’B’C’$~$ ∆ ABC.

Tính chất 3. Nếu  ∆A’B’C’ $~$∆ A”B”C”  và ∆A”B”C$~$ ∆ ABC thì ∆A’B’C’ $~$∆ ABC.

Ví dụ 6. Cho ∆A’B’C’$~$ ∆ ABC như hình vẽ. Tính tỉ số đồng dạng ?

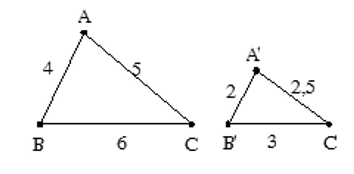
Lời giải:

Ta có ∆A’B’C’$~$ ∆ ABC. Khi đó tỉ số đồng dạng là

$\frac{A^{\text{'}}{B}^{\text{'}}}{AB}=\frac{A^{\text{'}}{C}^{\text{'}}}{AC}=\frac{B^{\text{'}}{C}^{\text{'}}}{BC}=\frac{2}{4}=\frac{2,5}{5}=\frac{3}{6}=\frac{1}{2}.$

4.2. Định lý

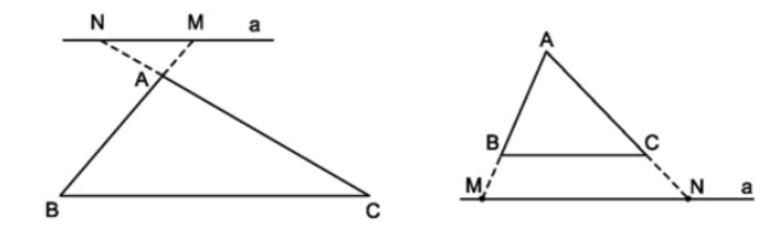
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

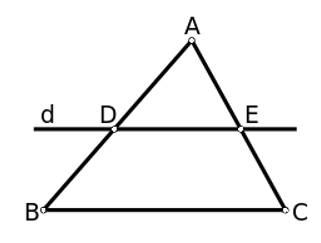
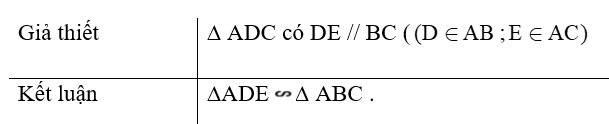
- Chú ý: Định lí cũng đúng cho trường hợp đường thẳng d cắt phần kéo dài của hai tam giác song song với cạnh còn lại.

5. Trường hợp đồng dạng thứ nhất.

5.1. Định lí

- Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.

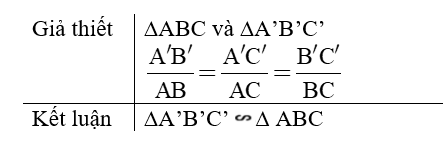
- Ví dụ 7.  Cho ∆ABC và ∆A’B’C’ có độ dài các cạnh như hình vẽ.

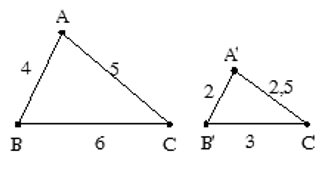
Ta có:

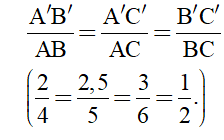
Do đó, ∆A’B’C’ $~$∆ ABC.

6. Trường hợp đồng dạng thứ hai

6.1. Định lí.

- Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng

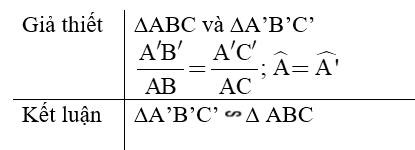
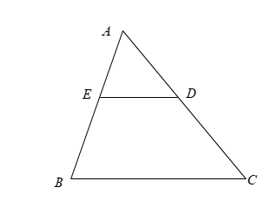
- Ví dụ 8. Cho tam giác ABC có AB = 15cm; AC = 20cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD = 8cm; AE = 6cm.

Chứng minh ∆AED $~$∆ ABC.

Lời giải:

Xét ∆AED và ∆ABC có:

  .

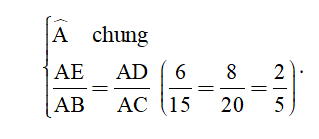Suy ra: ∆AED$~$ ∆ ABC.

7. Trường hợp đồng dạng thứ ba

7.1. Định lí

- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

- Ví dụ 9. Cho tam giác ABC và các đường cao BH, CK. Chứng minh ∆ABH $~$∆ ACK.  

Lời giải:

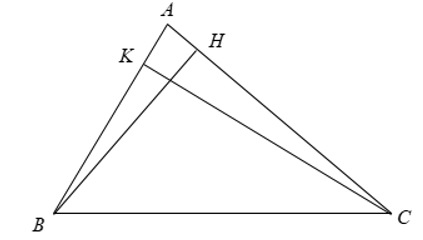
Xét ∆ABH và ∆ACK có:

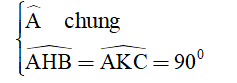
Suy ra: ∆ABH $~$∆ ACK.

8. Các trường hợp đồng dạng của tam giác vuông

8.1. Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông

Hai tam giác vuông đồng dạng với nhau nếu:

+ Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.

+ Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.

8.2. Dấu hiệu đặc biệt nhận biết hai tam vuông đồng dạng

- Định lý 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau 

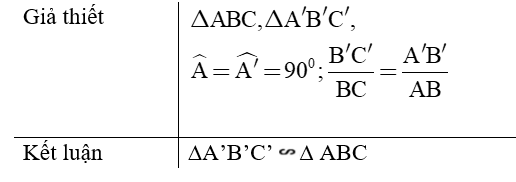
8.3. Tỉ số hai đường cao, tỉ số diện tích của hai tam giác đồng dạng

- Định lý 2: Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.

Cho hai tam giác ABC và A’B’C’ với tỉ số đồng dạng là $k=\frac{A\text{'}B\text{'}}{AB}$, hai đường cao tương ứng là AH và A’H’.

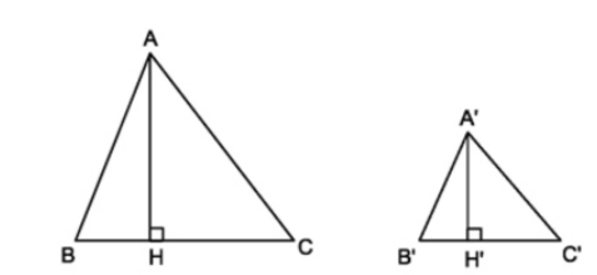
Khi đó, ta có tỉ số hai đường cao là : $\frac{h_{\Delta A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}}{h_{\Delta ABC}}=k$.

- Định lý 3: Tỉ số diện tích hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.

 
Ví dụ 10. Cho tam giác ABC đồng dạng với tam giác MNP theo tỉ số $k=\frac{2}{3}$ . Biết đường cao xuất phát từ A của tam giác ABC là AH = 12cm. Tính đường cao xuất phát từ M của tam giác MNP?

Lời giải:

Gọi đường cao xuất phát từ M của tam giác MNP là MK.

Vì tam giác ABC đồng dạng với tam giác MNP theo tỉ số $k=\frac{2}{3}$ nên $\frac{AH}{MK}=k\Rightarrow \frac{12}{MK}=\frac{2}{3}\Rightarrow MK=\frac{12.3}{2}=18$

Vậy MK = 18 cm.