 Giải bởi Vietjack
Giải bởi Vietjack
Điều kiện để A xác định: ⇔ (x - 1)(x - 9) ≠ 0 ⇔ x ≠ 1, x ≠ 9
Ta có:
Để A = 0 ⇔ 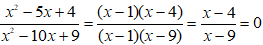
Vậy với x = 4 thì A = 0
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết