Cho hình vẽ dưới đây, biết đoạn thẳng JK song song và bằng đoạn thẳng ML.
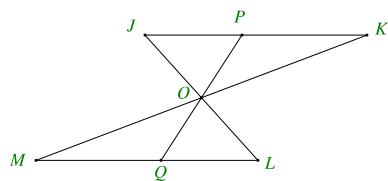
Khẳng định đúng là
Giải bởi Vietjack
Đáp án đúng là: C
Vì JK ∥ ML nên:
\(\widehat {{\rm{OJ}}K} = \widehat {OLM}\) (2 góc so le trong)
\(\widehat {{\rm{O}}KJ} = \widehat {OML}\) (2 góc so le trong)
Xét \(\Delta {\rm{JO}}K\) và \(\Delta LOM\) có:
\(\widehat {{\rm{OJ}}K} = \widehat {OLM}\) (chứng minh trên)
JK = ML (theo giả thiết)
\(\widehat {{\rm{O}}KJ} = \widehat {OML}\) (chứng minh trên)
Do đó \(\Delta JOK = \Delta LOM\) (g.c.g)
⇒ KO = MO (2 cạnh tương ứng)
Xét \(\Delta KOP\) và \(\Delta MOQ\) có:
\(\widehat {{\rm{O}}KJ} = \widehat {OML}\) (chứng minh trên)
KO = MO (chứng minh trên)
\(\widehat {KOP} = \widehat {MOQ}\) (2 góc đối đỉnh)
Do đó \(\Delta KOP = \Delta MOQ\) (g.c.g)
⇒ OP = OQ (2 cạnh tương ứng).
Vậy khẳng định C đúng.
Gói VIP thi online tại VietJack (chỉ 200k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC và tam giác DEF có AB = DE, AC = DF, \(\widehat A = \widehat D\). Biết \(\widehat B = 60^\circ \). Số đo góc E là
Cho tam giác ABC có AB = AC . Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chọn câu sai.
Cho tam giác ABC và tam giác MNP có \(\widehat A = \widehat P\); AC = MP, \[\widehat C = \widehat M\]. Phát biểu nào sau đây đúng?
Cho tam giác ABC và tam giác MNP có \(\widehat A = \widehat P\); AB = PN, AC = PM. Phát biểu nào sau đây đúng?
Cho tam giác ABC và tam giác \[NPM\] có BC = PM; \(\widehat B = \widehat P\). Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp cạnh – góc – cạnh?
Cho tứ giác ABCD, \[AB{\rm{//}}DC\], \[AD{\rm{//}}BC\], O là giao của AC và BD. Câu nào sau đây đúng?
Cho tam giác ABC và tam giác \[NPM\] có BC = PM; \(\widehat B = \widehat P\). Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp góc – cạnh – góc?
Cho góc xOy khác góc bẹt. Trên tia phân giác của góc xOy lấy điểm I tùy ý, qua I vẽ đường thẳng vuông góc với OI cắt Ox ở E và cắt Oy ở F. Trong các khẳng định sau, khẳng định nào đúng?
Cho hình vẽ sau, trong đó \(AB{\rm{//}}CD\), AB = CD. Khẳng định đúng là
Cho \[\Delta DEF\] có \(\widehat E = \widehat F\). Tia phân giác của góc D cắt EF tại I. Ta có
Cho hình vẽ dưới đây, biết CE = DE và \(\widehat {CEA} = \widehat {DEA}\).
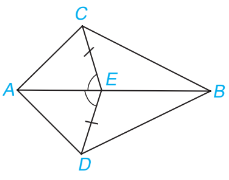
Khẳng định sai là
Cho tam giác ABC và tam giác DEF có AB = DE, \(\widehat B = \widehat E,{\rm{ }}\widehat A = \widehat D\). Biết AC = 6 cm. Độ dài DF là
