Rút gọn biểu thức với x 0 ta được kết quả là:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
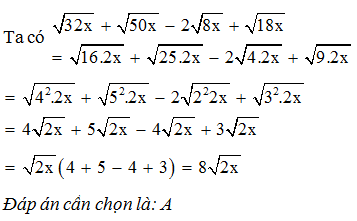
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Sau khi rút gọn biểu thức ta được phân số tối giản , (a, b ). Khi đó 2a có giá trị là:
1. Đưa một thừa số ra ngoài dấu căn
• Với a ≥ 0, b ≥ 0, ta có: . Phép biến đổi này được gọi là phép đưa thừa số ra ngoài dấu căn.
• Đôi khi, ta phải biến đổi biểu thức dưới dấu căn về dạng thích hợp rồi mới thực hiện được phép đưa thừa số ra ngoài dấu căn.
• Có thể sử dụng phép đưa thừa số ra ngoài dấu căn để rút gọn biểu thức chứa căn thức bậc hai.
Ví dụ 1.
a) ;
b) .
Tổng quát: Với hai biểu thức A, B mà B ≥ 0 ta có , tức là:
Nếu A ≥ 0 và B ≥ 0 thì ;
Nếu A < 0 và B ≥ 0 thì .
Ví dụ 2. Đưa thừa số ra ngoài căn:
a) với x ≥ 0, y < 0;
b) với x ≥ 0, y ≥ 0.
Lời giải:
a) (với x ≥ 0, y < 0);
b)
(với x ≥ 0, y ≥ 0).
2. Đưa thừa số vào trong dấu căn
• Phép đưa thừa số ra ngoài dấu căn có phép biến đổi ngược với nó là phép đưa thừa số vào trong dấu căn.
Với A ≥ 0 và B ≥ 0 thì .
Với A < 0 và B ≥ 0 thì .
Ví dụ 2. Đưa thừa số vào trong căn:
a) ;
b) với a ≥ 0.
Lời giải:
a) ;
b) với a ≥ 0.
• Có thể sử dụng phép đưa thừa số vào trong (hoặc ra ngoài) dấu căn để so sánh các căn bậc hai.
Ví dụ 3. So sánh và .
Lời giải:
Ta có: .
Vì nên .
3. Khử mẫu của biểu thức lấy căn
Tổng quát: Với các biểu thức A, B mà A. B ≥ 0 và B ≠ 0, ta có:
.
Ví dụ 4. Khử mẫu của biểu thức lấy căn
a) ;
b) với a > 0
Lời giải:
a) ;
b) Vì a > 0 nên 3a > 0. Do đó |3a| = 3a;
Vì a > 0 nên 9a3 > 0. Do đó
Khi đó,
.
4. Trục căn thức ở mẫu
Trục căn thức ở mẫu số là biến đổi để biểu thức đó mất căn thức ở mẫu số.
Tổng quát:
• Với các biểu thức A, B mà B > 0 ta có:
• Với các biểu thức A, B, C mà ta có:
.
• Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0, A ≠ B ta có:
.
Ví dụ 5. Trục căn thức ở mẫu
a) ;
b) .
Lời giải:
a)
.
b)
.