Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA=3a và SA vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
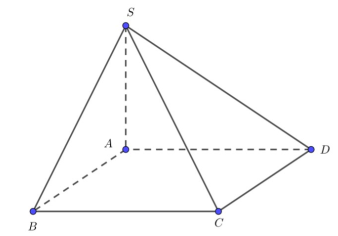
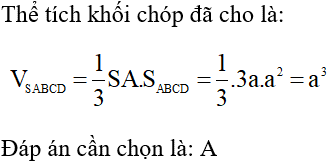
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên SC = 3a và SC vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng:
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại A, . Tam giác SBC đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là tứ giác đều cạnh a, biết rằng . Thể tích của khối lăng trụ?
Cho khối chóp S.ABCD có thể tích bằng , đáy ABCD là hình bình hành. Gọi M là trung điểm cạnh SD. Biết diện tích tam giác SAB bằng . Tính khoảng cách từ M tới mặt phẳng (SAB)
Cho khối chóp có chiều cao bằng 6, diện tích đáy bằng 4. Thể tích khối chóp đã cho bằng:
Cho hình lập phương ABCD.A'B'C'D' có diện tích mặt chéo ACC’A’ bằng . Thể tích của khối lập phương ABCD.A’B’C’D’ bằng:
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, SA vuông góc với đáy. Biết SA=BC=a, thể tích khối chóp S.ABC bằng:
Cho khối chóp có thể tích V, diện tích đáy là S và chiều cao h. Chọn công thức đúng:
Thể tích khối hộp chữ nhật có diện tích đáy S và độ dài cạnh bên a là:
Công thức tính thể tích lăng trụ có diện tích đáy S và chiều cao h là:
Lăng trụ đứng tứ giác có đáy là hình thoi mà các đường chéo là 6cm và 8cm, biết rằng chu vi đáy bằng 2 lần chiều cao lăng trụ. Tính thể tích khối lăng trụ
Cho hình chóp đều S.ABCD có cạnh AB = a, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng . Thể tích khối chóp S.ABCD là: