Cho hàm số f(x) = 3x – 2 có đồ thị (C). Điểm nào sau đây thuộc đồ thị hàm số (C).

+) y là hàm số của x được cho dưới dạng công thức:$y=\frac{1}{2}x$; y = x + 2; y = 5x.

• Hàm số thường được ký hiệu bởi những chữ f, g, h, ... chẳng hạn khi y là hàm số của biến số x, ta viết y = f(x) hoặc y = g(x), ….

• f(a) là giá trị của hàm số y = f(x) tại x = a. Khi hàm số y được cho bởi công thức y = f(x), muốn tính giá trị f(a) của hàm số tại x = a, ta thay x = a vào biểu thức f(x) rồi thực hiện các phép tính trong biểu thức.

Ví dụ 2. Ta có hàm số y = f(x) = 2x + 1.

Khi đó, f(2) = 2 . 2 + 1 = 5.

• Khi x thay đổi mà y luôn nhận một giá trị không đổi thì y được gọi là một hàm hằng.

Ví dụ 3. Ta có y = f(x) = 3.

Khi đó với giá trị nào của x thì y = 3.

Vậy y là hàm hằng.

2. Đồ thị của hàm số

Tập hợp các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ được gọi là đồ thị của hàm số y = f(x).

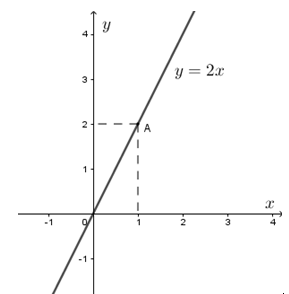
Ví dụ 4. Cho đồ thị của hàm số y = f(x) = 2x.

Các cặp giá trị tương ứng trên mặt phẳng tọa độ là O(0; 0); A(1; 2).

3. Hàm số đồng biến, nghịch biến

Cho hàm số y = f(x) xác định với mọi giá trị của x thuộc $ℝ$ .

• Nếu giá trị của biến x tăng lên mà giá trị của f(x) tương ứng cũng tăng lên thì hàm số y = f(x) được gọi là hàm số đồng biến trên R (gọi tắt là hàm số đồng biến).

• Nếu giá trị của biến x tăng lên mà giá trị của f(x) tương ứng giảm đi thì hàm số y = f(x) được gọi là hàm số nghịch biến trên R (gọi tắt là hàm số nghịch biến).

Nói cách khác, cho hàm số y = f(x) xác định trên tập số thực R. Với $x_1,x_2\in ℝ$  ta có:

+ Nếu x₁ < x₂ mà f(x₁) < f(x₂) thì hàm số đồng biến.

+ Nếu x₁ < x₂ mà f(x₁) > f(x₂) thì hàm số nghịch biến.

Ví dụ 5. Cho hàm số y = x – 5, xác định với $\forall x\in ℝ$ .

Ta có: x₁ < x₂ $\iff$ x₁ – 5 < x₂ – 5.

Hay f(x₁) < f(x₂) nên hàm số y = x – 5 đồng biến trên $ℝ$ .