Cho hai đường thẳng (d): và (d’) . Khi đó ta có hệ phương trình: (I). Số phát biểu đúng ?
(I). (d) cắt (d’) khi hệ phương trình (I) có nghiệm duy nhất
(II). (d) song song (d’) khi hệ phương trình (I) có vô số nghiệm
(III). (d) trùng với (d’) khi hệ phương trình (I) vô nghiệm
A. 0
B. 1
C. 2
D. 3
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Nếu (d) cắt (d’) thì hệ phương trình (I) có nghiệm duy nhất
Nếu (d) song song (d’) thì hệ phương trình (I) vô nghiệm
Nếu (d) trùng với (d’) thì hệ phương trình (I) có vô số nghiệm.
Do đó chỉ có phát biểu (I) đúng. Chọn B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Bạn Nga nhận xét: Hai hệ phương trình bậc nhất hai ẩn vô nghiệm thì tương đương với nhau.
Bạn Phương khẳng định: Hai hệ phương trình bậc nhất hai ẩn cùng có vô số nghiệm thì cũng luôn tương đương với nhau.
Nhận xét nào sau đây là đúng?
Hệ phương trình bậc nhất hai ẩn (các hệ số khác 0) vô nghiệm khi?
Cho hệ phương trình . Hệ phương trình nào trong các hệ sau tương đương với hệ phương trình đã cho
1. Khái niệm về hệ hai phương trình bậc nhất hai ẩn
Cho hai phương trình bậc nhất hai ẩn là ax + by = c và a'x + b'y = c'. Khi đó ta có hệ phương trình bậc nhất hai ẩn là:
Ví dụ 1:
; là các hệ hai phương trình bậc nhất hai ẩn.
+ Nếu hai phương trình có nghiệm chung là (x0; y0) thì (x0; y0) được gọi là một nghiệm của hệ phương trình (I).
+ Nếu hai phương trình không có nghiệm chung thì hệ phương trình (I) vô nghiệm.
+ Giải hệ phương trình là tìm tất cả các nghiệm của nó.
2. Minh họa hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn
Cho hai phương trình bậc nhất hai ẩn là ax + by = c và a'x + b'y = c'. Khi đó ta có hệ phương trình bậc nhất hai ẩn là:
Gọi (d) và (d') là đồ thị hàm số của 2 hàm số rút ra từ 2 phương trình bậc nhất hai ẩn của (I).
Đối với hệ phương trình (I), ta có:
Nếu (d) cắt (d') thì hệ (I) có một nghiệm duy nhất.
Nếu (d) song song với (d') thì hệ (I) vô nghiệm.
Nếu (d) trùng với (d') thì hệ (I) có vô số nghiệm.
Ví dụ 2: Xét hệ phương trình
Ta có: x – y = 0 (d)
x + y = 0 (d’)
Vẽ hai đường thẳng (d) và (d’) lên hệ trục tọa độ ta được:
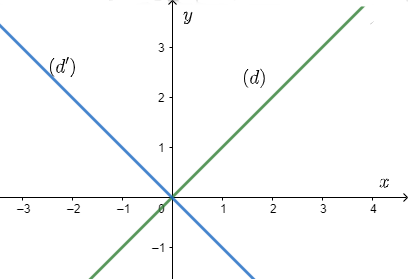
Ta thấy (d) và (d’) cắt nhau tại O(0; 0) nên (0; 0) là nghiệm của hệ phương trình.
Chú ý: Với trường hợp
Hệ phương trình có nghiệm duy nhất ;
Hệ phương trình vô nghiệm ;
Hệ phương trình vô số nghiệm .
3. Hệ phương trình tương đương
Định nghĩa: Hệ hai phương trình được gọi là tương đương với nhau nếu chúng có cùng một tập nghiệm.
Ta cũng dùng kí hiệu “” để chỉ sự tương đương của hai phương trình.