Cho hàm số y = a với a0. Kết luận nào sau đây là đúng.
A. Hàm số nghịch biến khi a > 0 và x > 0
B. Hàm số nghịch biến khi a < 0 và x < 0
C. Hàm số nghịch biến khi a > 0 và x < 0
D. Hàm số nghịch biến khi a > 0 và x = 0
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Cho hàm số y = a (a0)
a) Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0
b) Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Kết luận nào sau đây là sai khi nó về đồ thị của hàm số y = a với a0.
1. Đồ thị của hàm số
Định nghĩa: Đồ thị của hàm số là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol đỉnh O (với O là gốc tọa độ).
Tính chất:
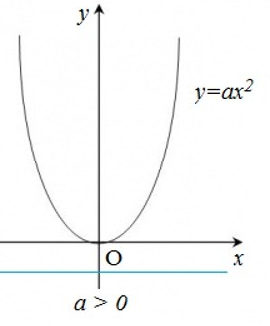
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
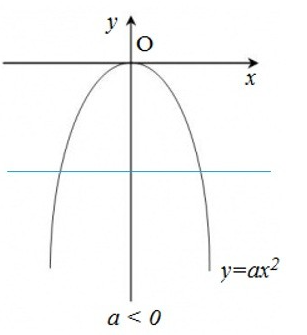
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
2. Cách vẽ đồ thị hàm số
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
Bước 3: Vẽ đồ thị và kết luận.
Chú ý: Vì đồ thị hàm số y = ax2 (a ≠ 0) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị của hàm số này, ta chỉ cần tìm một số điểm bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua Oy.