Một tam giác cân có đường cao ứng với đáy đúng bằng độ dài đáy. Tính các góc của tam giác đó.
A. ;
B. ;
C. ;
D. ;
 Giải bởi Vietjack
Giải bởi Vietjack
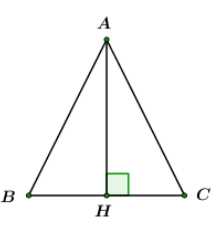
Giả sử BC = AH = a
Vì ABC là tam giác cân nên AH là đường cao đồng thời là đường trung tuyến
=> H là trung điểm BC => HB = HC =
Xét ABH vuông tại H ta có:
Vì ABC là tam giác cân
Ta có (định lý tổng ba góc trong một tam giác)
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC cân tại A, , đường cao CH = 3,6. Hãy giải tam giác ABC
Cho tam giác ABC vuông tại A có BC = 12cm, . Tính AC; (làm tròn đến chữ số thập phân thứ hai)
Cho tam giác ABC vuông tại A có BC = 26cm, AB = 10cm. Tính AC, (làm tròn đến độ)
Cho tam giác ABC vuông tại A có BC = 15cm, . Tính AC; (làm tròn đến chữ số thập phân thứ hai)
Cho tam giác ABC có , , AC = 3,5cm. Diện tích tam giác ABC gần nhất với giá trị nào dưới đây?
Cho tam giác ABC có , , AC = 4,5cm. Diện tích tam giác ABC gần nhất với giá trị nào dưới đây? (làm tròn đến chữ số thập phân thứ hai)
Cho tam giác ABC vuông tại A có BC = a, AC = b, . Chọn khẳng định đúng.
Tứ giác ABCD có , , AB = 4cm, AD = 3cm. Tính diện tích tứ giác ABCD (làm tròn đến chữ số thập phân thứ hai).
Cho tam giác DEF có DE = 7cm; ; . Kẻ đường cao EI của tam giác đó.
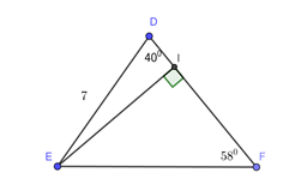
Hãy tính: (Kết quả làm tròn đến chữ số thập phân thứ 1). Đường cao EI:
Cho hình thang ABCD vuông tại A và D; . Biết AB = 2; AD = 1,2. Tính diện tích hình thang ABCD
Các hệ thức trong tam giác vuông:
Định lí. Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hay nhân với côsin góc kề.
+ Cạnh góc vuông kia nhân với tan của góc đối hay nhân với côtang của góc kề.
Ví dụ. Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c.
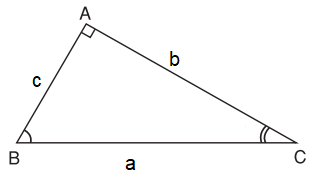
Khi đó, a là độ dài cạnh huyền;
b và c là độ dài hai cạnh góc vuông.
Do đó: b = a.sin B = a.cos C; c = a.sin C = a.cos B;
b = c.tan B = c.cot C; c = b.tan C = b.cot C.