Cho tam giác ABC vuông tại A, chiều cao AH. Chọn câu sai.
A. AH2 = BH. CH
B. AB2 = BH. BC
C.
D. AH. AB = BC. AC
 Giải bởi Vietjack
Giải bởi Vietjack
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
Định lí 1. Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Ví dụ 1. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
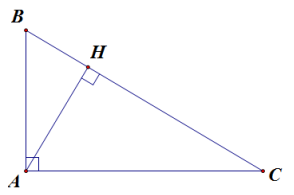
Ta có: AB2 = BC . BH; AC2 = BC . HC.
2. Một số hệ thức liên quan tới đường cao
Định lí 2. Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Ví dụ 2. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
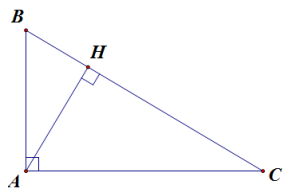
Ta có: AH2 = BH . HC.
Định lí 3. Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
Ví dụ 3. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
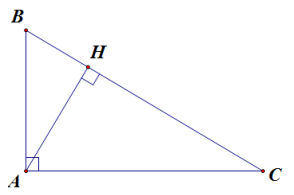
Ta có: AB . AC = BC . AH.
Định lí 4. Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
Ví dụ 4. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
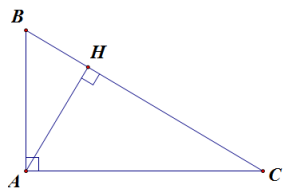
Ta có: .
3. Khái niệm tỉ số lượng giác của một góc nhọn
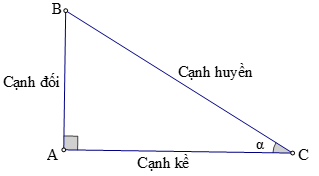
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sin α.
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cos α.
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tan α.
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cot α.
Ví dụ 1. Cho tam giác ABC có .
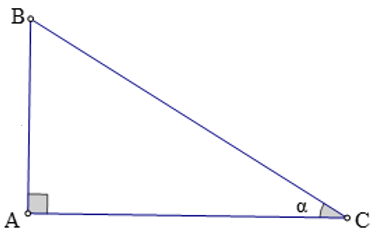
Khi đó: ; ; ;
Nhận xét: Nếu α là một góc nhọn thì:
0 < sin α < 1; 0 < cos α < 1; tan α > 0; cot α > 0.
Ví dụ 2. Cho tam giác ABC có

Khi đó: ; ; ;
Chú ý: Nếu hai góc nhọn α và β có sin α = sin β (hoặc cos α = cos β, hoặc tan α = tan β, hoặc cot α = cot β) thì α = β vì chúng là hai góc tương ứng của hai tam giác vuông đồng dạng.
Ví dụ 3. Cho tam giác ABC có AB = AC, đường cao AH. MN là đường trung bình của tam giác ABH. Chứng minh .
Lời giải:
Vì AH là đường cao của ∆ABC nên hay (1)
Mà MN là đường trung bình của ∆AMN nên:
+ AB = 2AM; AH = 2AN.
+ MN // BH (2)
Từ (1) và (2) suy ra (tính chất từ vuông góc đến song song).
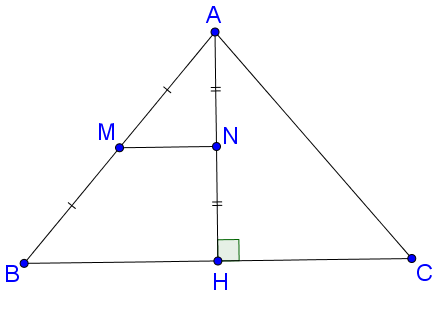
Xét ∆AMN vuông tại N (vì ) nên: .
Xét ∆ACH vuông tại H nên: .
Ta thấy: .
Do đó (đpcm).
4. Tỉ số lượng giác của hai góc phụ nhau
Định lí. Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Ví dụ 4. Cho tam giác ABC vuông tại A có .
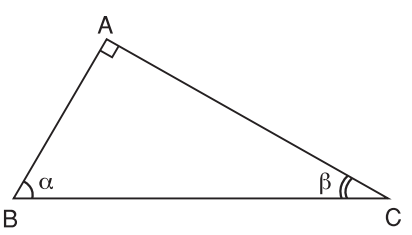
Khi đó, α + β = 90° (trong tam giác vuông hai góc nhọn phụ nhau).
Ta có: sin α = cos β; cos α = sin β; tan α = cot β; cot α = tan β.
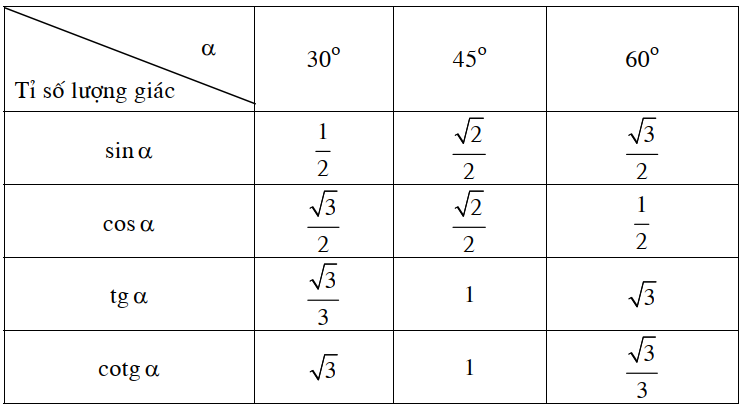
Bảng lượng giác của một số góc đặc biệt:
Ví dụ 5. Cho tam giác ABC vuông tại A có BC = 16, . Tính độ dài AB.
Lời giải:
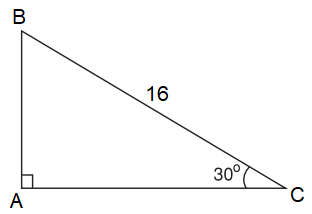
Xét ∆ABC vuông tại A, ta có: .
Hay .
Suy ra .
Vậy AB = 8 (đvđd).
Chú ý: Từ nay khi viết các tỉ số lượng giác của một góc nhọn trong tam giác, ta bỏ kí hiệu " ^ " đi.
Ví dụ 6. Góc A là góc nhọn thì ta viết sin A thay cho .
5. Các hệ thức trong tam giác vuông:
Định lí. Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hay nhân với côsin góc kề.
+ Cạnh góc vuông kia nhân với tan của góc đối hay nhân với côtang của góc kề.
Ví dụ. Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c.
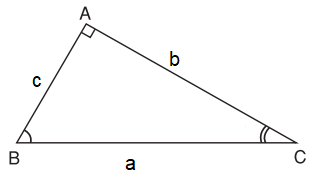
Khi đó, a là độ dài cạnh huyền;
b và c là độ dài hai cạnh góc vuông.
Do đó: b = a.sin B = a.cos C; c = a.sin C = a.cos B;
b = c.tan B = c.cot C; c = b.tan C = b.cot C.