Cho hình chữ nhật ABCD. Tìm khẳng định đúng
A. AC < BD
B. AB > AC
C. AC > CD
D. AB > BD
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Gọi I là giao điểm hai đường chéo AC và BD,
Theo tính chất hình chữ nhật ta có:
Do đó, I là tâm đường tròn ngoại tiếp hình chữ nhật ABCD có AC và BD là đường kính.
AB, BC, CD và DA là các dây.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết rằng khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng
Cho đường tròn tâm O có dây AB = 16cm. Gọi M là trung điểm AB. Biết khoảng cách từ O đến AB bằng 6. Tính bán kính đường tròn.
Cho đường tròn tâm O , bán kính R = 5cm , có dây AB = 8cm và M là trung điểm của AB. Tính khoảng cách từ O đến AB?
Cho đường tròn (O) có bán kính R = 5 cm. Khoảng cách từ tâm đến dây AB là 3 cm. Tính độ dài dây AB
Cho đường tròn (O) đường kính AB và dây CD không đi qua tâm. Khẳng định nào sau đây là đúng?
Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn
“Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì…với dây ấy”. Điền vào dấu…cụm từ thích hợp
Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính BC.
1. So sánh độ dài của đường kính và dây
Định lí 1. Trong các dây của một đường tròn, dây lớn nhất là đường kính.
Ví dụ 1. Gọi AB là một dây bất kỳ của đường tròn (O; R).
Chứng minh rằng AB ≤ 2R.
Lời giải:
* Trường hợp 1: AB là đường kính.
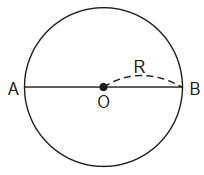
Khi đó, AB = 2R (1)
* Trường hợp 2: AB không là đường kính.
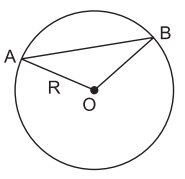
Áp dụng bất đẳng thức tam giác vào ∆AOB, ta có:
AB < AO + OB = R + R = 2R (2)
Từ (1) và (2) suy ra AB ≤ 2R (đpcm).
2. Quan hệ vuông góc giữa đường kính và dây
Định lí 2. Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó.
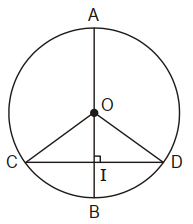
Ví dụ 2. Cho đường tròn (O) đường kính AB. Dây CD của đường tròn (O). Biết tại I.
Khi đó, IC = ID (như hình vẽ).
Định lí 3. Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
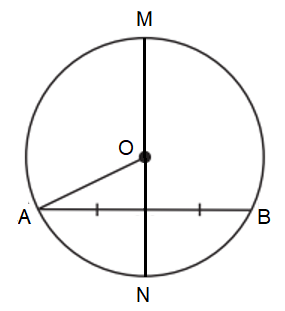
Ví dụ 3. Cho đường tròn (O) đường kính MN và dây AB. Đường kính MN đi qua trung điểm của dây AB.
Khi đó (như hình vẽ).