Cho đường tròn (O; R), có dây cung MN có độ dài là 24cm, khoảng cách từ O đến đường thẳng MN là 16cm. Độ dài bán kính R là?
A. 24cm
B. 25cm
C. 16cm
D. 20cm
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Độ dài bán kính của đường tròn là:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đường tròn (O;5cm). Dây AB và CD song song, có độ dài lần lượt là 8cm và 6cm. Biết OM, ON theo thứ tự là khoảng cách từ tâm đến dây AB và CD. Tính tổng OM và ON?
Cho đường tròn (O) đường kính AB. Kẻ hai dây AC và BD song song. Chọn khẳng định đúng trong các khẳng định sau.
Cho đường tròn (O) đường kính AB = 13 cm, dây CD có độ dài 12 cm vuông góc với AB tại H ( H nằm giữa O và A). Tính HB.
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm (O). Tìm khẳng định đúng?
Cho đường tròn tâm O, bán kính R = 10cm. Tam giác ABC nội tiếp đường tròn tâm O, biết góc A là góc tù. Hỏi trong các dây AB, BC và AC thì dây nào gần tâm nhất?
Cho đường tròn (O; R = 20). Cho dây cung MN có độ dài 36. Khoảng cách từ tâm O đến dây cung là?
Cho đường tròn tâm O, bán kính R = 6cm ngoại tiếp tam giác ABC vuông tại A có AB = 6cm, AC = 8 cm. Trong các dây AB, BC và AC thì dây nào gần tâm hơn?
Cho đường tròn tâm O bán kính 3 cm và hai dây AB và AC. Biết AB = 5cm, AC = 2cm. Trong 2 dây AB và AC dây nào gần tâm hơn?
Cho đường tròn (O; R = 25). Khi đó dây cung lớn nhất của đường tròn đó bằng?
1. Định lý 1.
Định lý 1. Trong một đường tròn:
a) Hai dây bằng nhau thì cách đều tâm.
b) Hai dây cách đều tâm thì bằng nhau.
Ví dụ 1. Cho đường tròn (O), hai dây AB và CD.
Gọi OH, OK lần lượt là khoảng cách từ tâm O đến dây AB và CD.
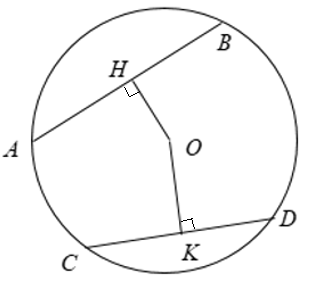
Khi đó:
+ Nếu AB = CD thì OH = OK.
+ Nếu OH = OK thì AB = CD.
Vậy AB = CD ⇔ OH = OK.
2. Định lý 2
Định lý 2. Trong hai dây của một đường tròn:
a) Dây nào lớn hơn thì dây đó gần tâm hơn.
b) Dây nào gần tâm hơn thì dây đó lớn hơn.
Ví dụ 2. Cho đường tròn (O), hai dây AB và CD.
Gọi OH, OK lần lượt là khoảng cách từ tâm O đến dây AB và CD.
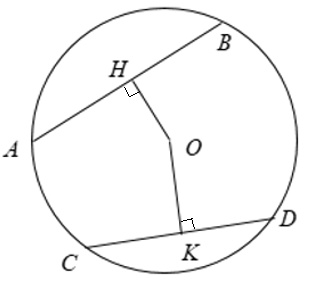
Khi đó:
+ Nếu AB > CD thì dây gần tâm O hơn dây CD hay OH < OK.
+ Nếu OH < OK thì AB > CD.
Vậy OH < OK ⇔ AB > CD.