Cho đường tròn (O; R). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn với (E; F là tiếp điểm). Đoạn OM cắt đường tròn (O; R) tại I. Kẻ đường kính ED của (O; R). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK. Cho FK = 4cm. Khi đó:
A. FP = PK = 2cm
B. P là trọng tâm tam giác FDE
C. A, B đều đúng
D. A, B đều sai
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
* Vì ME là tiếp tuyến của (O) nên ME vuông góc với OE, suy ra tam giác MOE nội tiếp đường tròn đường kính MO (1)
Vì MF là tiếp tuyến của (O) nên MF vuông góc với OF, suy ra tam giác MOF nội tiếp đường tròn đường kính MO (1)
Từ (1) và (2) suy ra M, E, O, F cùng thuộc một đường tròn.
* Gọi MO EF = {H}
Vì M là giao điểm của hai tiếp tuyến ME và MF của (O)
ME = MF (tính chất) mà OE = OF = R (gt)
MO là đường trung trực của EF
MO EF
Gọi G là giao điểm của tia DF và tia EM
Ta có (góc nội tiếp chắn nửa đường tròn) EF DG mà
EF OM (cmt) OM // DG (từ vuông góc đến song song)
Tam giác EDG có OE = OD; OM // DG ME = MG (tính chất đường trung bình)
Áp dụng định lý Ta-lét cho tam giác EDM có OK // ME (cùng vuông góc với ED) ta được: (3)
Áp dụng định lý Ta-lét cho tam giác MDG có PF// MG (cùng vuông góc với ED) ta được: (4)
Từ (3) và (4) suy ra mà ME = MG (cmt)
PK = PF P là trung điểm của FK. Suy ra
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đường tròn (O; R). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn với (E; F là tiếp điểm). Đoạn OM cắt đường tròn (O; R) tại I. Kẻ đường kính ED của (O; R). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK. Chọn câu đúng:
Cho đường tròn (O; R) và điểm A nằm ngoài (O). Từ A, kẻ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với (O) (E không trùng với D). Số đo góc HEC là:
1. Định lý về hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
• Điểm đó cách đều hai tiếp điểm.
• Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
• Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
Ví dụ 1. Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Từ điểm A kẻ hai tiếp tuyến AB và AC (B và C là tiếp điểm). Khi đó:
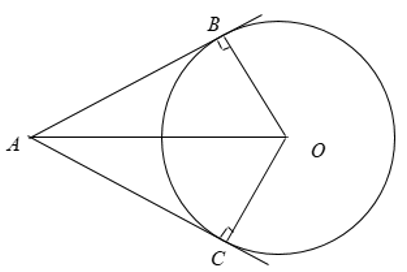
• Điểm A cách đều hai tiếp điểm B và C hay AB = AC.
• AO là tia phân giác của .
• OA là tia phân giác của .
2. Đường tròn nội tiếp của tam giác
Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác, còn tam giác gọi là tam giác ngoại tiếp đường tròn.
Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác.
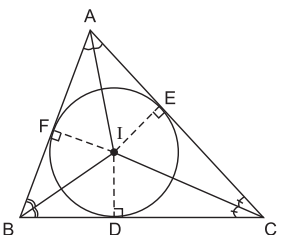
Ví dụ 2. Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB.
Khi đó, I là tâm đường tròn nội tiếp tam giác ABC hay tam giác ABC ngoại tiếp đường tròn tâm I.
3. Đường tròn bàng tiếp tam giác
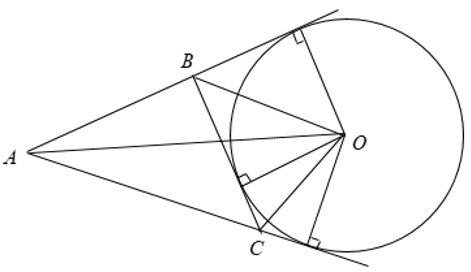
Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia.
Tâm của đường tròn bàng tiếp trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, hoặc là giao điểm của đường phân giác góc A và đường phân giác góc ngoài tại B (hoặc C).
Với một tam giác, có ba đường tròn bàng tiếp.
Ví dụ 3. Cho tam giác ABC. Gọi K là giao điểm các đường phân giác của hai góc ngoài tại B và C; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ K đến các đường thẳng BC, AC, AB.
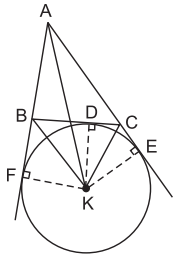
Khi đó, K là tâm đường tròn bàng tiếp tam giác ABC.