Cho hai đường tròn tiếp xúc ngoài (O; R) và (O’; r) với R > r và OO’ = d. Chọn khẳng định đúng
A. d = R – r
B. d > R + r
C. R – r < d < R + r
D. d = R + r
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Hai đường tròn (O) và (O’) tiếp xúc ngoài nên hệ thức liên hệ d = R + r
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Nếu hai đường tròn tiếp xúc nhau thì số điểm chung của hai đường tròn là:
Nếu hai đường tròn không cắt nhau thì số điểm chung của hai đường tròn là:
Cho hai đường tròn (O; R) và (O’; r) với R > r cắt nhau tại hai điểm phân biệt và OO’ = d. Chọn khẳng định đúng
Cho đoạn OO’ và điểm A nằm trên đoạn OO’ sao cho OA = 2O’A. Đường tròn (O) bán kính OA và đường tròn (O’) bán kính O’A. Vị trí tương đối của hai đường tròn là:
Cho đường tròn (O) bán kính OA và đường tròn (O’) đường kính O’A. Nếu OO’= |OA – O’A| thì:
1. Ba vị trí tương đối của hai đường tròn
a) Hai đường tròn cắt nhau
Hai đường tròn có hai điểm chung được gọi là hai đường tròn cắt nhau. Hai điểm chung đó gọi là hai giao điểm. Đoạn thẳng nối hai điểm đó gọi là dây chung.
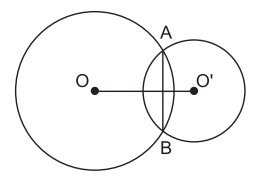
Ví dụ 1. Hai đường tròn (O) và (O’) có hai điểm chung A và B.
Khi đó, ta nói hai đường tròn (O) và (O’) là hai đường tròn cắt nhau.
Hai điểm chung A và B gọi là hai giao điểm.
Đoạn thẳng AB là dây chung.
b) Hai đường tròn tiếp xúc nhau
Hai đường tròn chỉ có một điểm chung được gọi là hai đường tròn tiếp xúc nhau. Điểm chung đó gọi là tiếp điểm.
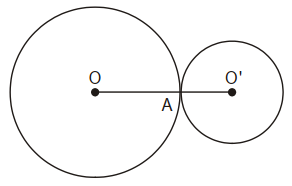
Ví dụ 2. Hai đường tròn (O) và (O’) có một điểm chung là A.
Khi đó, ta nói hai đường tròn (O) và (O’) là hai đường tròn tiếp xúc nhau.
Điểm chung A được gọi là tiếp điểm.
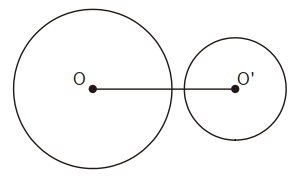
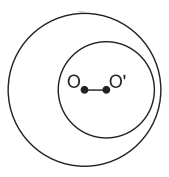
c) Hai đường tròn không giao nhau
Hai đường tròn không có điểm chung nào được gọi là hai đường tròn không giao nhau.
2. Tính chất đường nối tâm
Cho hai đường tròn (O) và (O’) có tâm không trùng nhau. Đường thẳng OO’ gọi là đường nối tâm, đoạn thẳng OO’ gọi là đoạn nối tâm.
Do đường kính là trục đối xứng của mỗi đường tròn nên đường nối tâm là trục đối xứng của hình gồm cả hai đường tròn đó.
Tính chất đường nối tâm: Đường nối tâm là đường trung trực của dây chung.
Ví dụ 3. Hai đường tròn (O; R) và (O’; r) cắt nhau có hai điểm chung A và B.
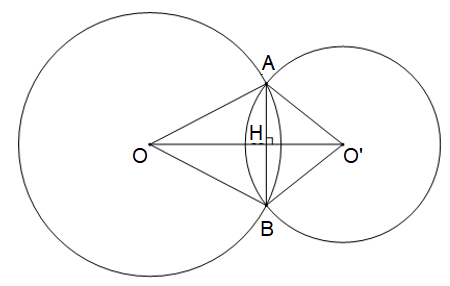
Khi đó, đường thẳng OO’ là đường nối tâm, đoạn thẳng OO’ là đoạn nối tâm.
Đường thẳng nối tâm OO’ là đường trung trực của dây chung AB.
Định lí.
• Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây chung.
• Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
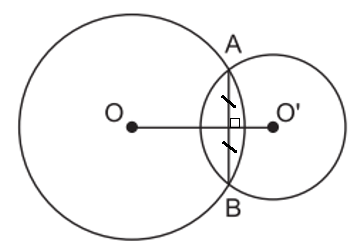
Ví dụ 4. Hai đường tròn (O; R) và (O’; r) cắt nhau có hai điểm chung A và B.
Khi đó, hai giao điểm A và B đối xứng nhau qua đường nối tâm OO’.
Hay đường nối tâm OO’ là đường trung trực của dây chung AB.
3. Hệ thức giữa đoạn nối tâm và các bán kính
a) Hai đường tròn cắt nhau
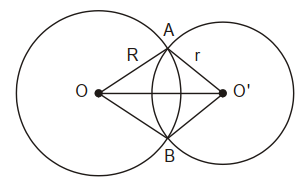
Hai đường tròn (O) và (O’) cắt nhau tại A và B.
Khi đó: |R − r| < OO’ < R + r.
b) Hai đường tròn tiếp xúc nhau
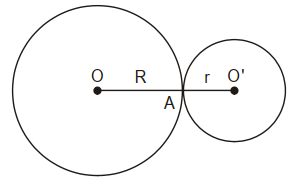
Hai đường tròn (O) và (O’) tiếp xúc nhau tại A.
• Nếu hai đường tròn (O) và (O’) tiếp xúc ngoài tại A, khi đó tiếp điểm A nằm giữa O và O’.
Do đó: OO’ = R + r.
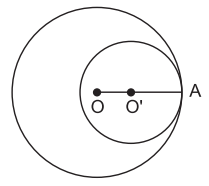
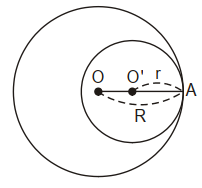
• Nếu hai đường tròn (O) và (O’) tiếp xúc trong tại A, khi đó tiếp điểm O’ nằm giữa O và A.
Do đó: OO’ = |R − r|.
b) Hai đường tròn không giao nhau
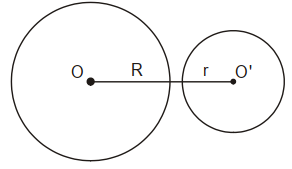
Hai đường tròn (O) và (O’) không giao nhau.
• Hai đường tròn (O) và (O’) ở ngoài nhau: OO’ > R + r.
• Đường tròn (O) đựng đường tròn (O’): OO’ < |R − r|.
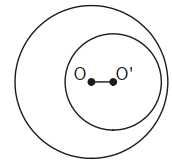
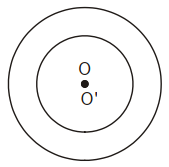
• Đặc biệt, khi hai tâm trùng nhau, ta nói hai đường tròn đồng tâm: OO’ = 0.
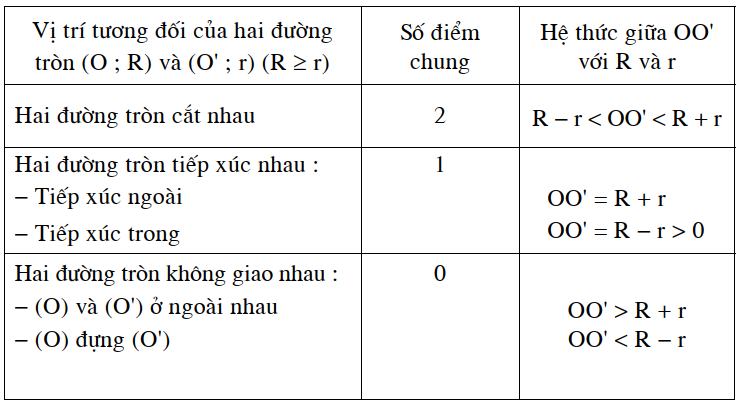
Ta có bảng sau:
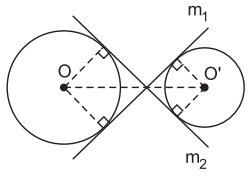
4. Tiếp tuyến chung của hai đường tròn
Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó.
• Các đường thẳng d1 và d2 là các tiếp tuyến chung ngoài của hai đường tròn (O) và (O’) (tiếp tuyến chung ngoài không cắt đoạn nối tâm).
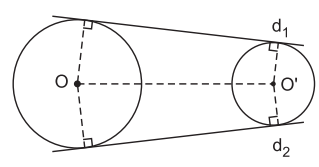
• Các đường thẳng m1 và m2 là các tiếp tuyến chung trong của hai đường tròn (O) và (O’) (tiếp tuyến chung trong cắt đoạn nối tâm).