Cho tam giác đều ABC. Vẽ đường tròn (I) đường kính BC cắt cạnh AB, AC lần lượt tại D và E
a) Tính số đo mỗi cung BD (cung lớn và cung nhỏ)
b) Chứng tỏ rằng
 Giải bởi Vietjack
Giải bởi Vietjack
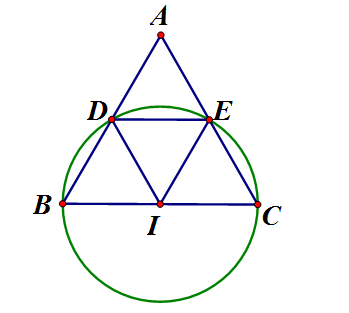
a) Ta có: IB = ID = R và đều nên sđ BD nhỏ nên số đo cung BC lớn
b) Chứng minh tương tự đều nên sđ cung EC
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đường tròn (O; R), các dây AB, CD, EF có độ dài như sau , Tính số đo các cung
Cho hệ phương trình
Tìm các giá trị của a, b để hệ phương trình có nghiệm là (1; -3)
Cho đường tròn (O) đường kính AB, vẽ góc ở tâm với C nằm trên (O). Vẽ dây CD vuông góc với AB và dây DE song song với AB
a) Tính số đo cung nhỏ
b) Tính số đo cung Từ đó suy ra 3 điểm C, O, E thẳng hàng.
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa A vẽ nửa đường tròn đường kính BC. D là điểm trên nửa đường tròn sao cho Gọi M là giao điểm của AD và BC. Chứng minh rằng BM = 2MC.
Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = 2R. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm)
a) Tính
b) Tính và số đo cung AB nhỏ .
Cho tam giác ABC cân tại A. Vẽ đường tròn tâm O, đường kính BC. Đường tròn (O) cắt AB, AC lần lượt tại M, N
a) Chứng minh
b) Tính biết