Cho hình vẽ:
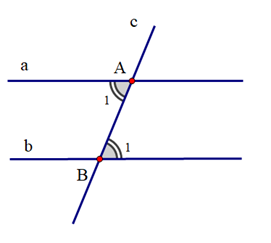
Hãy phát biểu định lí sau bằng lời:
|
GT |
Đường thẳng c cắt hai đường thẳng a, b lần lượt tại A và B; a // b |
|
KL |
\({\widehat A_1} = {\widehat B_1}\) |
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: C
Bảng trên được phát biểu như sau: Nếu đường thẳng c cắt hai đường thẳng song song a và b lần lượt tại hai điểm A và B thì hai góc so le trong \({\widehat A_1}\) và \({\widehat B_1}\) bằng nhau.
Một cách tổng quát ta có định lí: Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau.
Vậy ta chọn phương án C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Khi học bài “Định lí và chứng minh định lí”, cô giáo yêu cầu học sinh lấy ví dụ về các định lí. Ba bạn An, Khánh, Bình phát biểu như sau:
An: Định lí “Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng còn lại”.
Khánh: Định lí “Nếu qua điểm M nằm ngoài đường thẳng a có hai đường thẳng song song với a thì chúng trùng nhau”.
Bình: Định lí “Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”
Theo em, bạn nào phát biểu đúng về định lí?
Cho định lí: “Hai tia phân giác của hai góc kề bù thì vuông góc với nhau” được minh hoạ bởi hình vẽ sau:
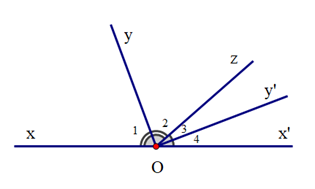
Giả thiết của định lí trên là
Cho các khẳng định sau:
(I). Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các cặp góc đồng vị bằng nhau;
(II). Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau;
(III). Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bù nhau.
Có bao nhiêu định lí trong các khẳng định trên?