Dạng 1. Nhận biết như thế nào là một định lí và xác định giả thiết, kết luận của định lí có đáp án
-
670 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Hướng dẫn giải:
- Khẳng định trên là một định lí vì:
+ Khẳng định trên chính là tính chất của hai góc đối đỉnh: “Hai góc đối đỉnh thì bằng nhau”.
+ Khẳng định được phát biểu dưới dạng: Nếu…thì…
Câu 2:
Xem đáp án
Hướng dẫn giải:
- Giả thiết là: hai góc kề bù;
- Kết luận là: hai góc đó có tổng bằng 180°.
Câu 3:
Trong các câu sau, câu nào cho ta một định lí?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
- Câu A: “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” là khẳng định được suy ra từ khẳng định đúng đã biết là: “Nếu hai đường thẳng phân biệt cùng cắt một đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì chúng song song với nhau”.
Thật vậy:
Giả sử hai đường thẳng a, b phân biệt cùng vuông góc với đường thẳng c như hình vẽ:
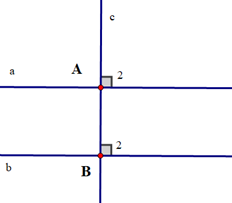
Ta có a \( \bot \) c; b \( \bot \) c
Suy ra a // b.
Vậy câu A là một định lí.
- Câu B, C không đầy đủ hai phần giả thiết (là những điều cho biết trước) và kết luận (những điều cần suy ra).
- Câu D là một khẳng định sai.
Do đó các câu B, C, D không là các định lí.
Câu 4:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Xét định lí: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau” ta có:
- Phần giữa từ “Nếu” và từ “thì” là: một đường thẳng cắt hai đường thẳng song song.
- Phần sau từ “thì” là: hai góc đồng vị bằng nhau.
Vậy giả thiết là: một đường thẳng cắt hai đường thẳng song song;
Kết luận là: hai góc đồng vị bằng nhau.
Câu 5:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Câu A là khẳng định sai vì hai góc bằng nhau chưa chắc đã đối đỉnh.
Ví dụ:
Do đó câu A không phải là một định lí.
Câu 6:
Cho các khẳng định sau:
(I). Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các cặp góc đồng vị bằng nhau;
(II). Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau;
(III). Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bù nhau.
Có bao nhiêu định lí trong các khẳng định trên?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
+ Theo dấu hiệu nhận biết hai đường thẳng song song, ta có: nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau. Khi đó theo tính chất của hai đường thẳng song song ta có các cặp góc đồng vị bằng nhau.
Suy ra khẳng định (I) đúng.
Suy ra khẳng định (I) là một định lí.
+ Theo dấu hiệu nhận biết hai đường thẳng song song, ta có: Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng đó song song với nhau. Khi đó theo tính chất của hai đường thẳng song song ta có các cặp góc so le trong bằng nhau.
Suy ra khẳng định (II) đúng, khẳng định (III) sai.
Suy ra khẳng định (II) là một định lí, khẳng định (III) không là một định lí.
Do đó có 2 định lí trong các khẳng định trên.
Câu 7:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Định lí: Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
Vậy ta chọn phương án C.
Câu 8:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Giả thiết là phần đứng trước từ “thì” nên ta có giả thiết của định lí này là: Hai đường thẳng song song.
Vậy ta chọn phương án B.
Câu 9:
Cho hình vẽ:
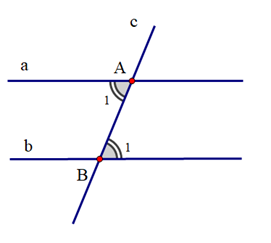
Hãy phát biểu định lí sau bằng lời:
|
GT |
Đường thẳng c cắt hai đường thẳng a, b lần lượt tại A và B; a // b |
|
KL |
\({\widehat A_1} = {\widehat B_1}\) |
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Bảng trên được phát biểu như sau: Nếu đường thẳng c cắt hai đường thẳng song song a và b lần lượt tại hai điểm A và B thì hai góc so le trong \({\widehat A_1}\) và \({\widehat B_1}\) bằng nhau.
Một cách tổng quát ta có định lí: Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau.
Vậy ta chọn phương án C.
Câu 10:
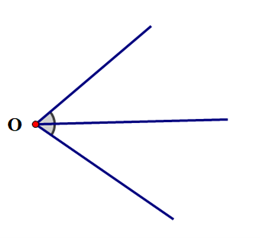
Cho định lí: “Hai tia phân giác của hai góc kề bù thì vuông góc với nhau” được minh hoạ bởi hình vẽ sau:
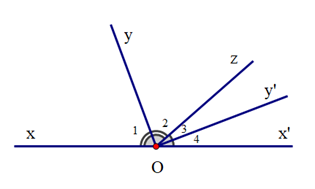
Giả thiết của định lí trên là
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Giả thiết: Oy là tia phân giác của \(\widehat {xOz}\); Oy’ là tia phân giác của \(\widehat {zOx'}\); \(\widehat {xOz}\) và \(\widehat {zOx'}\) là hai góc kề bù.
Câu 11:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Ta có hai định lí:
+ Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
+ Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Vậy ta chọn phương án C.
Câu 12:
Khi học bài “Định lí và chứng minh định lí”, cô giáo yêu cầu học sinh lấy ví dụ về các định lí. Ba bạn An, Khánh, Bình phát biểu như sau:
An: Định lí “Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng còn lại”.
Khánh: Định lí “Nếu qua điểm M nằm ngoài đường thẳng a có hai đường thẳng song song với a thì chúng trùng nhau”.
Bình: Định lí “Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”
Theo em, bạn nào phát biểu đúng về định lí?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
+ Khẳng định “Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng còn lại” là một định lí.
Do đó An đúng.
+ Khẳng định: “Nếu qua điểm M nằm ngoài đường thẳng a có hai đường thẳng song song với a thì chúng trùng nhau” là một định lý vì nó được suy ra từ tiên đề Euclid.
Do đó Khánh đúng.
+ Khẳng định: “Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” là khẳng định sai vì trong trường hợp hai đường thẳng trùng nhau cùng vuông góc với đường thẳng thứ ba thì chúng không song song với nhau.
Suy ra khẳng định của Bình không là một định lí.
Do đó Bình sai.
Vậy chỉ có An và Khánh đúng.