Lựa chọn đáp án đúng nhất:
Phân tích đa thức thành nhân tử, ta được:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
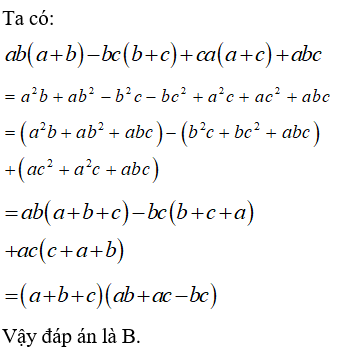
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Lựa chọn đáp án đúng nhất:
Khẳng định dưới đây đúng hay sai:
Với thì
Lựa chọn đáp án đúng nhất:
Phân tích đa thức thành nhân tử, ta được:
Lựa chọn đáp án đúng nhất:
Khẳng định dưới đây đúng hay sai:
Với thì là bình phương một số nguyên.
Lựa chọn đáp án đúng nhất:
Phân tích đa thức thành nhân tử thì sẽ có một nhân tử là:
Lựa chọn đáp án đúng nhất:
Phân tích đa thức thành nhân tử thì sẽ có một nhân tử là:
Khái niệm: Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.
Phương pháp: Khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.
- Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho nhân tử chung.