Cho đoạn thẳng AB. Gọi d là đường trung trực của AB. Trên đường thẳng d lấy điểm M bất kì. Trong mặt phẳng lấy đểm C sao cho BC < CA.
a) So sánh MB + MC với CA;
b) Tìm vị trí của M trên d sao cho MB + MC nhỏ nhất.
 Giải bởi Vietjack
Giải bởi Vietjack
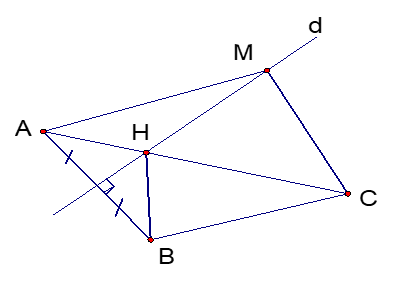
a) M thuộc đường trung trực d của AB nên MA = MB (tính chất đường trung trực của đoạn thẳng)
Suy ra MB + MC = MA + MC.
Trong tam giác MAC, ta có: MA + MC > AC.
Vậy MB + MC > AC (0,5 điểm)
b) Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d.
Nên A và C nằm trong hai nửa mặt phẳng bờ d khác nhau.
Do đó d cắt AC tại H.
Vậy khi M H thì: MB + MC = HB + HC = HA + HC
=> MB + MC = AC
Vậy ta có MB + MC AC
Khi M trùng với H thì HB + HC = AC.
Tức là MB + MC nhỏ nhất khi M H là giao điểm của AC với d.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hai đa thức:
R(x) = x2 + 5x4 – 2x3 + x2 + 6x4 + 3x3 – x + 15
H(x) = 2x – 5x3 – x2 – 2x4 + 4x3 – x2 + 3x – 7
a) Thu gọn rồi sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến;
b) Tính R(x) + H(x) và R(x) – H(x).Tìm nghiệm của các đa thức
a) P(x) = 5x – 3; b) F(x) = (x + 2)(x – 1).
Cho ABC cân tại A ( nhọn ). Tia phân giác góc của A cắt BC tại I.
a) Chứng minh AI BC;
b) Gọi M là trung điểm của AB, G là giao điểm của CM với AI. Chứng minh rằng BG là đường trung tuyến của tam giác ABC;
c) Biết AB = AC = 15cm; BC = 18 cm. Tính GI.
a) Thu gọn và tìm bậc của đa thức;
b) Tính giá trị của đa thức tại x = 1 và y = –1.
Thời gian (Tính bằng phút) giải một bài toán của học sinh lớp 7A được thầy giáo bộ môn ghi lại như sau
|
4 |
8 |
4 |
8 |
6 |
6 |
5 |
7 |
5 |
3 |
6 |
7 |
|
7 |
3 |
6 |
5 |
6 |
6 |
6 |
9 |
7 |
9 |
7 |
4 |
|
4 |
7 |
10 |
6 |
7 |
5 |
4 |
6 |
6 |
5 |
4 |
8 |
a) Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
b) Lập bảng “tần số” và tìm Mốt của dấu hiệu;
c) Tính số trung bình cộng của dấu hiệu