Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 9
-
4512 lượt thi
-
6 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Thời gian (Tính bằng phút) giải một bài toán của học sinh lớp 7A được thầy giáo bộ môn ghi lại như sau
|
4 |
8 |
4 |
8 |
6 |
6 |
5 |
7 |
5 |
3 |
6 |
7 |
|
7 |
3 |
6 |
5 |
6 |
6 |
6 |
9 |
7 |
9 |
7 |
4 |
|
4 |
7 |
10 |
6 |
7 |
5 |
4 |
6 |
6 |
5 |
4 |
8 |
a) Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
b) Lập bảng “tần số” và tìm Mốt của dấu hiệu;
c) Tính số trung bình cộng của dấu hiệu Xem đáp án
Xem đáp án
a) Dấu hiệu ở đây là thời gian (tính bằng phút) giải một bài toán toán của mỗi học sinh.
Số các giá trị là: N = 36. (0,5 điểm)
b) Bảng tần số:
|
Giá trị (x) |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Tần số (n) |
2 |
6 |
5 |
10 |
7 |
3 |
2 |
1 |
N = 36 |
Mốt của dấu hiệu là: M0 = 6. (0,5 điểm)
c) Số trung bình cộng của dấu hiệu là:
Câu 2:
a) Thu gọn và tìm bậc của đa thức;
b) Tính giá trị của đa thức tại x = 1 và y = –1.
 Xem đáp án
Xem đáp án
a) Ta có
M = 3x6y + x4y3 – 4y7 – 4x4y3 + 11 – 5x6y + 2y7 – 2
=
=
=
Thay x = 1 và y = –1 vào đa thức ta được:
Câu 3:
Cho hai đa thức:
R(x) = x2 + 5x4 – 2x3 + x2 + 6x4 + 3x3 – x + 15
H(x) = 2x – 5x3 – x2 – 2x4 + 4x3 – x2 + 3x – 7
a) Thu gọn rồi sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến;
b) Tính R(x) + H(x) và R(x) – H(x). Xem đáp án
Xem đáp án
a) Thu gọn rồi sắp xếp theo lũy thừa giảm dần của biến, ta được:
R(x) = x2 + 5x4 – 2x3 + x2 + 6x4 + 3x3 – x + 15
=
= (0,5 điểm)
H(x) = 2x – 5x3 – x2 – 2x4 + 4x3 – x2 + 3x – 7
=
= –2x4 – x3 – 2x2 + 5x – 7 (0,5 điểm)
b, Ta có:
R(x) + H(x) = C + (–2x4 – x3 – 2x2 + 5x – 7)
=
=
= 9x4 + 4x + 8
R(x) – H(x) = – (–2x4 – x3 – 2x2 + 5x – 7)
=
=
Câu 4:
Tìm nghiệm của các đa thức
a) P(x) = 5x – 3; b) F(x) = (x + 2)(x – 1).
 Xem đáp án
Xem đáp án
a) P(x) = 5x – 3 có nghiệm 5x – 3 = 0 x = (0,5 điểm)
b) F(x) = (x + 2)(x – 1) có nghiệm (x + 2)(x – 1) = 0
x + 2 = 0 hoặc x – 1 = 0 x = –2 hoặc x = 1 (0,5 điểm)
Câu 5:
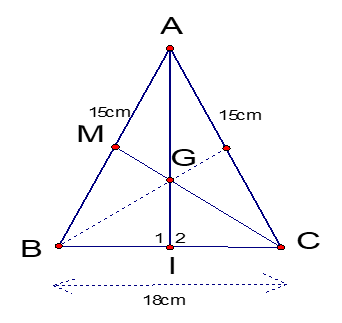
Cho ABC cân tại A ( nhọn ). Tia phân giác góc của A cắt BC tại I.
a) Chứng minh AI BC;
b) Gọi M là trung điểm của AB, G là giao điểm của CM với AI. Chứng minh rằng BG là đường trung tuyến của tam giác ABC;
c) Biết AB = AC = 15cm; BC = 18 cm. Tính GI.
 Xem đáp án
Xem đáp án
- Vẽ hình đúng và ghi GT, KL đúng. (0,5 điểm)
a) Xét tam giác AIB và tam giác AIC có:
AB = AC (tam giác ABC cân tại A)
AI là cạnh chung
(AI là tia phân giác của góc A)
Do đó: tam giác AIB = tam giác AIC (cgc) (Hai góc tương ứng)
Mà (Hai góc kề bù) . (1 điểm)
b) Ta có: MA = MB (M là trung điểm của AB)
=> CM là đường trung tuyến ứng với cạnh AB.
Trong tam giác cân ABC (cân tại A), AI là đường phân giác ứng với đáy BC
=> AI cũng là đường trung tuyến
Do đó G là giao của hai trung tuyến AI và CM nên G là trọng tâm của tam giác ABC (Tính chất ba đường trung tuyến của tam giác)
Nên BG là đường trung tuyến của tam giác ABC. (1 điểm)
c) Trong tam giác cân ABC (Cân tại A), AI là phân giác cũng là trung tuyến
Nên IB = IC = BC IB = IC = 9 (cm)
Áp dụng định lí Py–ta–go vào tam giác vuông AIB, ta có:
AI2 = AB2 – IB2 = 152 – 92 = 144 => AI = 12 (cm)
G là trọng tâm của tam giác ABC => GI = AI = . 12 = 4 (cm) (0,5 điểm)
Câu 6:
Cho đoạn thẳng AB. Gọi d là đường trung trực của AB. Trên đường thẳng d lấy điểm M bất kì. Trong mặt phẳng lấy đểm C sao cho BC < CA.
a) So sánh MB + MC với CA;
b) Tìm vị trí của M trên d sao cho MB + MC nhỏ nhất.
 Xem đáp án
Xem đáp án
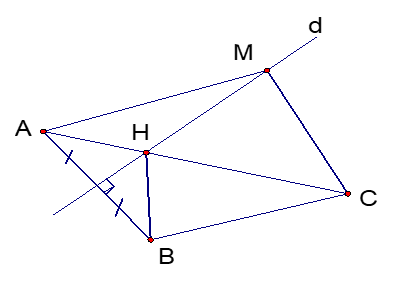
a) M thuộc đường trung trực d của AB nên MA = MB (tính chất đường trung trực của đoạn thẳng)
Suy ra MB + MC = MA + MC.
Trong tam giác MAC, ta có: MA + MC > AC.
Vậy MB + MC > AC (0,5 điểm)
b) Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d.
Nên A và C nằm trong hai nửa mặt phẳng bờ d khác nhau.
Do đó d cắt AC tại H.
Vậy khi M H thì: MB + MC = HB + HC = HA + HC
=> MB + MC = AC
Vậy ta có MB + MC AC
Khi M trùng với H thì HB + HC = AC.
Tức là MB + MC nhỏ nhất khi M H là giao điểm của AC với d.
