Tìm giá trị của a để biểu thức ( a2x3 + 3ax2 - 6x - 2a ) chia hết cho ( x + 1 )
 Giải bởi Vietjack
Giải bởi Vietjack
Do ( a2x3 + 3ax2 - 6x - 2a ) chia hết cho ( x + 1 ) nên ta có thể viết như sau:
( a2x3 + 3ax2 - 6x - 2a ) = ( mx2 + nx + p )( x + 1 ) ( 1 )
Trong đó thương ( mx2 + nx + p ) là một tam thức bậc ha.
Ta thấy ( 1 ) đúng với mọi giá trị của x, nên cũng đúng với x = - 1
Do đó ta có: - a2 + 3a + 6 - 2a = 0 ⇔ - a2 + a + 6 = 0⇔
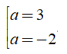
Vậy để ( a2x3 + 3ax2 - 6x - 2a ) chia hết cho ( x + 1 ) thì giá trị của a là a =3 hoặc a = -2
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Chứng tỏ rằng các biểu thức sau không phụ thuộc vào biến x
a, x( 2x + 1 ) - x2( x + 2 ) + ( x3 - x + 3 )
Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B với:
A = 7xn - 1y5 - 5x3y4;
B = 5x2yn
Giá trị nhỏ nhất của biểu thức 9x2 - 6x + 5 đạt được khi x bằng ?
Rút gọn biểu thức ( a - b )3 + ( a + b )3 - a( 6b2 + 2a2 ) được kết quả là ?