 Giải bởi Vietjack
Giải bởi Vietjack
Đặt = α , = β ⇒ = α + β
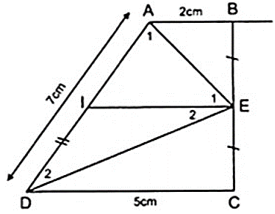
Do E là trung điểm của BC theo giả thiết vẽ I là trung điểm của AD thì AI = ID = = 3,5( cm ). (1 )
Ta có EI là đường trung bình của hình thang ABCD.
Áp dụng định lý đường trung bình của hình thang ABCD ta có:
IE = = 3,5( cm ) ( 2 )
Từ ( 1 ) và ( 2 ) ta có
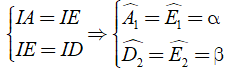
(vì trong tam giác, đối diện với hai cạn bằng nhau là hai góc bằng nhau)
+ Xét tam giác ADE có = 1800
Hay α + α + β + β = 2( α + β ) = 1800 ⇒ α + β = 900
Do α + β = 900 nên = 900.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tính chiều cao của hình thang cân ABCD, biết rằng cạnh bên AD = 5cm, cạnh đáy AB = 6cm và CD = 14cm.
Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC.
a) Chứng minh rằng BI ⊥ AK.
Cho hình thang vuông ABCD có = 900 và CD = 2AB. Kẻ DE ⊥ AC, gọi I là trung điểm của EC. Chứng minh rằng = 900.
Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, qua A kẻ AN ⊥ AM (điểm N thuộc tia đối của tia DC). Gọi I là trung điểm của MN. Chứng minh rằng:
a) AM = AN