Bất phương trình \[\left( {x + 1} \right)\left( {x + 4} \right) < 5\sqrt {{x^2} + 5x + 28} \] có nghiệm là
A.\[ - 9 < x \le 4\]
B. \[ - 9 < x < 4\]
C. \[ - 9 < x < - 4\]
D. \[ - 9 < x < - 1\]Trả lời:
Giải bởi Vietjack
TXĐ: \[D = \mathbb{R}\]\[\left( {x + 1} \right)\left( {x + 4} \right) < 5\sqrt {{x^2} + 5x + 28} \Leftrightarrow {x^2} + 5x + 4 - 5\sqrt {{x^2} + 5x + 28} < 0\](1)
Đặt \[\sqrt {{x^2} + 5x + 28} = t\left( {t >0} \right)\]
(1) trở thành:\[{t^2} - 5t - 24 < 0 \Leftrightarrow - 3 < t < 8\]
\[ \Rightarrow {x^2} + 5x + 28 < 64 \Leftrightarrow {x^2} + 5x - 36 < 0 \Leftrightarrow - 9 < x < 4\]
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
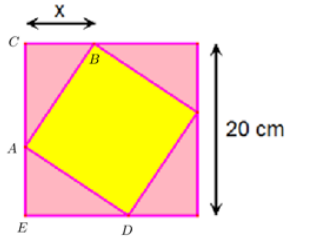
Một viên gạch hình vuông có cạnh thay đổi được đặt nội tiếp trong một hình vuông có cạnh bằng 20cm, tạo thành bốn tam giác xung quanh như hình vẽ.
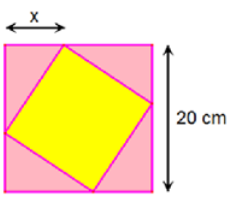
Tìm tập hợp các giá trị của x để diện tích viên gạch không vượt quá 208cm2.
Cho biểu thức \[f\left( x \right) = \left( {x + 5} \right)\left( {3 - x} \right).\]Tập hợp tất cả các giá trị của x thỏa mãn bất phương trình f(x) ≤ 0 là
Bất phương trình \[\sqrt { - {x^2} + 6x - 5} >8 - 2x\]có nghiệm là:
Tập nghiệm SS của bất phương trình \[5x - 1 \ge \frac{{2x}}{5} + 3\]là:
Tổng các nghiệm nguyên của bất phương trình \(\frac{{x - 2}}{{\sqrt {x - 4} }} \le \frac{4}{{\sqrt {x - 4} }}\) bằng:
Tổng các nghiệm nguyên của bất phương trình \[x\left( {2 - x} \right) \ge x\left( {7 - x} \right) - 6\left( {x - 1} \right)\] trên đoạn \[\left[ { - 10;10} \right]\;\]bằng:
Hỏi có bao nhiêu giá trị nguyên x trong \[\left[ { - 2017;2017} \right]\;\]thỏa mãn bất phương trình \[|2x + 1| < 3x\;\]?
Bạn An chọn một số nguyên, nhân số đó với 4 rồi trừ đi 30. Lấy kết quả có được nhân với 2 và cuối cùng trừ đi 10 thì được một số có hai chữ số. Số lớn nhất An có thể chọn được có hàng đơn vị bằng:
Để bất phương trình \[\sqrt {(x + 5)(3 - x)} \le {x^2} + 2x + a\] nghiệm đúng \[\forall x \in [ - 5;3]\]tham số a phải thỏa điều kiện:
\[\sqrt {\left( {x + 5} \right)\left( {3 - x} \right)} \le {x^2} + 2x + a \Leftrightarrow \sqrt { - {x^2} - 2x + 15} - {x^2} - 2x \le a\]
Tập nghiệm của bất phương trình \[\left| {x - 3} \right| >- 1\]là
Tập nghiệm của bất phương trình: \[ - {x^2} + 6x + 7\; \ge 0\;\] là:
Tập nghiệm của bất phương trình \[2x\left( {4 - x} \right)\left( {3 - x} \right)\left( {3 + x} \right) >0\]là
