ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Hàm số bậc hai
-
2051 lượt thi
-
27 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Đường thẳng nào trong các đường thẳng sau đây là trục đối xứng của parabol
 Xem đáp án
Xem đáp án
Ta có:
Trục đối xứng là đường thẳng: Đáp án cần chọn là: C
Câu 2:
Đỉnh I của parabol (P): là:
 Xem đáp án
Xem đáp án
Ta có:
Suy ra đỉnh của Parabol là: I(1;2)
Đáp án cần chọn là: A
Câu 3:
Biết parabol (P): đi qua điểm A(2;1). Giá trị của aa là:
 Xem đáp án
Xem đáp án
Parabol đi qua điểm A(2;1) nên ta có:4a + 4 + 5 = 1 ⇔ 4a = −8 ⇔ a = −2
Đáp án cần chọn là: B
Câu 4:
Đỉnh của parabol nằm trên đường thẳng nếu m bằng:
 Xem đáp án
Xem đáp án
Yêu cầu bài toán
Đáp án cần chọn là: D
Câu 5:
Bảng biến thiên của hàm số là:
 Xem đáp án
Xem đáp án
Ta có:
Suy ra bảng biến thiên:
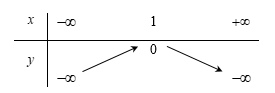
Đáp án cần chọn là: C
Câu 7:
Tìm tọa độ giao điểm của hai parabol: và là:
 Xem đáp án
Xem đáp án
Trả lời:
Phương trình hoành độ giao điểm của hai parabol :
Tọa độ giao điểm
Đáp án cần chọn là: C
Câu 8:
Cho hàm số . Gọi M và m là giá trị lớn nhất vá giá trị nhỏ nhất của hàm số trên [0;2]. Tính giá trị của biểu thức .
 Xem đáp án
Xem đáp án
Hàm số có Hàm số đồng biến trên và nghịch biến trên
BBT:
![Cho hàm số . Gọi M và m là giá trị lớn nhất vá giá trị nhỏ nhất của hàm số trên [0;2]. Tính giá trị của biểu thức . (ảnh 1)](https://video.vietjack.com/upload2/images/1652760013/1652760196-image50.png)
Dựa vào BBT ta thấy M = 2 và
Đáp án cần chọn là: A
Câu 9:
Hàm số nào sau đây có giá trị nhỏ nhất tại ?
 Xem đáp án
Xem đáp án
Trả lời:
Hàm số đạt GTNN nếu a >0 nên loại phương án B và C.
Phương án A: Hàm số có giá trị nhỏ nhất tại nên loại.
Còn lại chọn phương án D.
Đáp án cần chọn là: D
Câu 10:
Cho hàm số . Mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Ta có a = −1 < 0 nên hàm số y tăng trên và y giảm trên nên chọn phương án A.
Đáp án cần chọn là: A
Câu 11:
Hàm số nào sau đây nghịch biến trong khoảng
 Xem đáp án
Xem đáp án
Đáp án A: và nên hàm số nghịch biến trên
Đáp án B: và nên hàm số đồng biến trên
Đáp án C: có và nên hàm số nghịch biến trên nhưng nên hàm số không nghịch biến trên
Đáp án D: có và nên hàm số nghịch biến trên
Vậy chỉ có đáp án A đúng.
Đáp án cần chọn là: A
Câu 12:
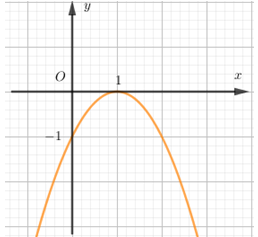
Hình vẽ bên là đồ thị của hàm số nào?
 Xem đáp án
Xem đáp án
- Đồ thị hàm số đi qua điểm (1;0) nên loại A và C.
- Bề lõm hướng xuống dưới nên a < 0.
Đáp án cần chọn là: B
Câu 13:
Giao điểm của parabol với trục hoành:
 Xem đáp án
Xem đáp án
- Xét phương trình hoành độ giao điểm:
- Phương trình có hai nghiệm nên các giao điểm là (−1;0),(−4;0).
Đáp án cần chọn là: A
Câu 14:
Khi tịnh tiến parabol sang trái 3 đơn vị, ta được đồ thị của hàm số:
 Xem đáp án
Xem đáp án
Tịnh tiến đồ thị hàm số sang trái 3 đơn vị ta được đồ thị hàm số .
Đáp án cần chọn là: A
Câu 15:
Tìm giá trị thực của tham số để hàm số có giá trị nhỏ nhất bằng −10 trên R.
 Xem đáp án
Xem đáp án
Ta có suy ra
Hàm số có giá trị nhỏ nhất bằng −10
Đáp án cần chọn là: B
Câu 16:
Nếu hàm số có a < 0,b >0 và c >0 thì đồ thị của nó có dạng:
 Xem đáp án
Xem đáp án
+ a < 0 nên loại đáp án A, B.
+ c >0 nên giao điểm của đồ thị với trục tung có tung độ dương, chọn đáp án D.
Ngoài ra các em cũng có thể nhận xét vì b >0, a < 0 nên hoành độ đỉnh và đáp án D thỏa mãn.
Đáp án cần chọn là: D
Câu 17:
Cho parabol (P): . Khẳng định đúng nhất trong các khẳng định sau là:
 Xem đáp án
Xem đáp án
- Ta có a = − 3< 0 và
- Đường thẳng x = 1 là trục đối xứng.
- Đồ thị hàm số cắt trục Oy ⇒ x = 0 ⇒ y = −1
Đáp án cần chọn là: D
Câu 18:
Cho parabol (P): biết rằng parabol đó cắt trục hoành tại hai điểm lần lượt có hoành độ và . Parabol đó là:
 Xem đáp án
Xem đáp án
- Parabol (P)cắt Ox tại A(1;0), B(2;0).
- Khi đó
Vậy
Đáp án cần chọn là: D
Câu 19:
Cho hàm số có đồ thị (P). Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Hàm số đồng biến trên khoảng và nghịch biến trên khoảng Nên A, B sai.
Ta chưa kết luận được gì về số giao điểm của đồ thị hàm số đã cho với trục hoành nên C sai.
Đồ thị hàm số có trục đối xứng là đường thẳng nên D đúng.
Đáp án cần chọn là: D
Câu 20:
Cho hàm số biết hàm số đạt giá trị lớn nhất trên bằng 4 khi x = -1 và tổng bình phương các nghiệm của phương trình y = 0 bằng 10. Hàm số đã cho là hàm số nào sau đây?
 Xem đáp án
Xem đáp án
Hàm số là hàm số bậc 2 nên có đỉnh Vì hàm số đạt giá trị lớn nhất trên  bằng 4 khi x = −1 nên đồ thị hàm số có đỉnh I(−1;4) và a < 0.
bằng 4 khi x = −1 nên đồ thị hàm số có đỉnh I(−1;4) và a < 0.
Xét phương trình: có hai nghiệm
Áp dụng định lý Vi-et ta có:
Theo đề bài ta có:
Đáp án cần chọn là: D
Câu 21:
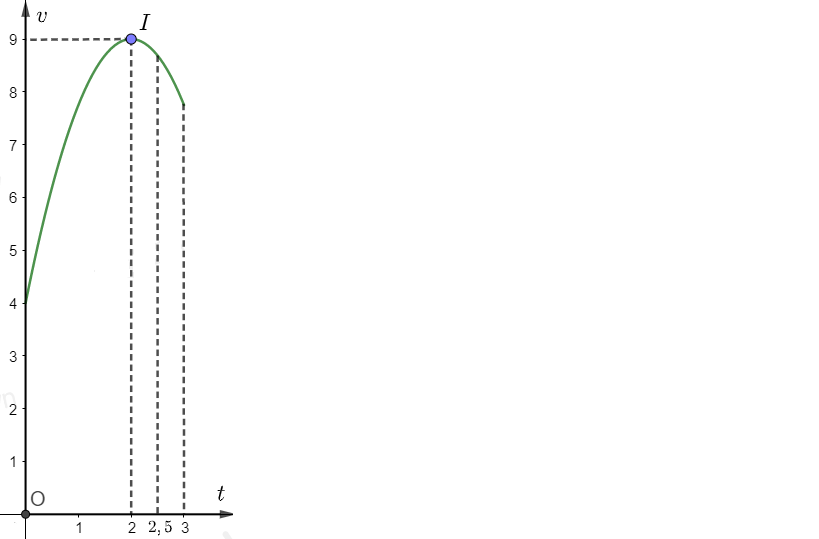
Một vật chuyển động trong 3 giờ với vận tốc v(km/h) phụ thuộc thời gian t(h) có đồ thị là một phần của parabol có đỉnh I(2;9) và trục đối xứng song song với trục tung như hình vẽ. Vận tốc của vật tại thời điểm 2 giờ 30 phút sau khi vật bắt đầu chuyển động gần bằng giá trị nào nhất trong các giá trị sau?
 Xem đáp án
Xem đáp án
Vì vận tốc v(km/h) phụ thuộc thời gian t(h) có đồ thị là một phần của parabol nên ta có hàm số
Dựa vào đồ thị hàm số ta có: tại thời điểm t = 0, v = 4
Đồ thị hàm số có đỉnh I(2;9)⇒
Tại lúc 2 giờ 30 phút = 2,5 giờ vận tốc đạt được là:
Đáp án cần chọn là: A
Câu 22:
Một vật được ném lên trên cao và độ cao của nó so với mặt đất được cho bởi công thức , với t là thời gian tính bằng giây (s) kể từ lúc bắt đầu ném. Độ cao cực đại mà vật đó có thể đạt được so với mặt đất bằng bao nhiêu mét?
 Xem đáp án
Xem đáp án
Ta có có đồ thị là parabol có bề lõm hướng xuống, đạt GTLN tại
Vậy
Câu 23:
Parabol đạt cực tiểu bằng 4 tại x = −2 và đi qua A(0;6) có phương trình là:
y = … x2+ … x + ….
 Xem đáp án
Xem đáp án
Parabol đạt cực đại bằng 4 khi x = −2 ⇒ parabol có đỉnh I(−2;4)
Lại có parabol đi qua điểm A(0;6) nên ta có:
Vậy parabol đã cho có hàm số
Câu 24:
Tập hợp các giá trị của tham số m để hàm số đồng biến trên khoảng là
 Xem đáp án
Xem đáp án
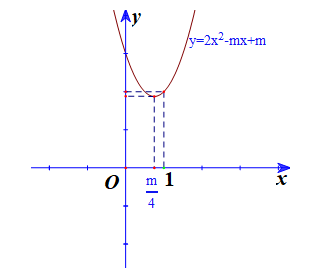
Hàm số đồng biến trên nên để hàm số đồng biến trên thì
Vậy
Đáp án cần chọn là: A
Câu 25:
Giá trị lớn nhất của hàm số là:
 Xem đáp án
Xem đáp án
Đồ thị hàm số có đỉnh I(2;3) và có hệ số a < 0 ⇒ Hàm số đạt GTLN bằng 3 khi x = 2.
Câu 26:
Giá trị lớn nhất của hàm số là:
 Xem đáp án
Xem đáp án
Bước 1: Xác định hệ số a
Ta có a = −1 < 0
Hàm số đã cho đạt giá trị lớn nhất tại
Bước 2: Tìm giá trị của hàm số tại tìm m.
Khi đó
Để Maxy = 6 thì m – 4 = 6 ⇔ m = 10
Câu 27:
Ký hiệu M và m tương ứng là GTLN và GTNN của hàm số trên miền . Biết rằng M = km. Tìm k?
 Xem đáp án
Xem đáp án
Bước 1:
Xét hàm số trên ta có BBT:
Đỉnh của đồ thị hàm số là I(1;4)
Ta thấy Ta lập bảng biến thiên:
Bước 2:
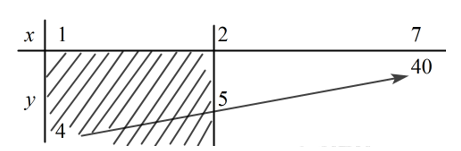
Dựa vào BBT ta có: khi x = 7 và khi x = 2.
⇒M = 8m
