Cho hàm số Tập hợp tất cả các giá trị của m để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt có hoành độ âm là:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:
Để đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt có hoành độ âm thì phương trình (∗) có 2 nghiệm âm phân biệt khác −1
Đáp án cần chọn là: A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
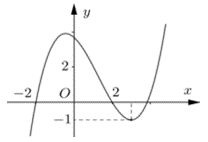
Cho hàm số liên tục trên và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm?
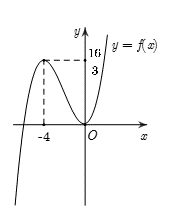
Cho hàm số có đồ thị (C).Để đồ thị (C) cắt trục hoành tại ba điểm A,B,C sao cho C là trung điểm của AB thì giá trị của tham số m là:
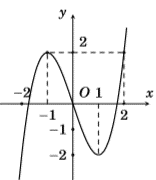
Cho hàm số f(x) có bảng biến thiên như sau:
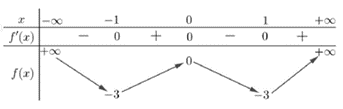
Phương trình có bao nhiêu nghiệm thực?
Tìm m để đồ thị hàm số cắt đường thẳng tại ba điểm phân biệt có hoành độ thỏa mãn
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn của tham số m để đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt?
Cho hàm số liên tục trên và có đồ thị như hình vẽ bên. Số nghiệm của phương trình là:
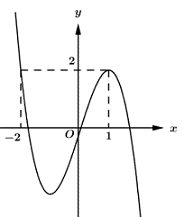
Cho hàm số . Giá trị của tham số m để đường thẳng cắt tại ba điểm phân biệt sao cho tam giác KBC có diện tích bằng với điểm là:
Cho hàm số xác định trên liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
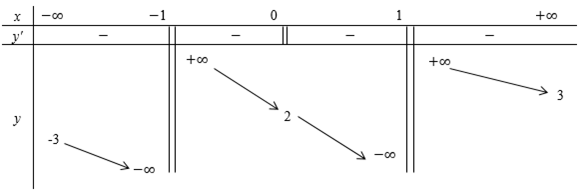
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt.
Cho hàm số liên tục trên R và có bảng biến thiên như hình vẽ
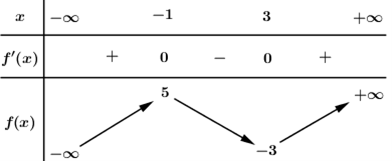
Phương trình có bao nhiêu nghiệm?
Cho hàm số bậc ba có đồ thị như hình vẽ bên. Số nghiệm của phương trình là:
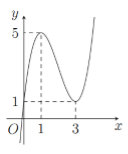
Cho hai đồ thị hàm số và đồ thị hàm số có tất cả bao nhiêu điểm chung?