Bài toán tương giao đồ thị
-
556 lượt thi
-
33 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
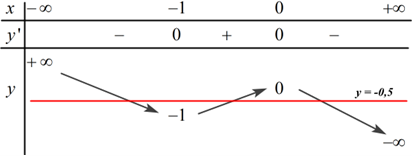
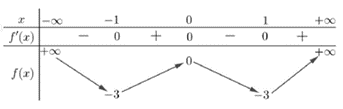
Cho hàm số y=f(x) xác định trên R∖{−1;1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
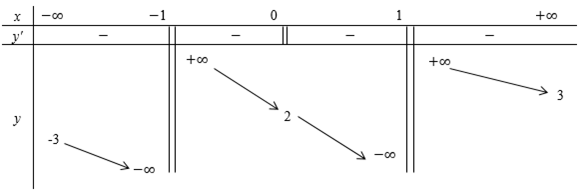
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng y=2m+1 cắt đồ thị hàm số tại hai điểm phân biệt.
 Xem đáp án
Xem đáp án
Quan sát BBT ta thấy đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt ⇔
Đáp án cần chọn là: C
Câu 2:
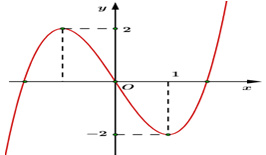
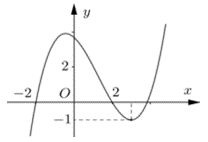
Cho hàm số bậc ba có đồ thị như hình vẽ bên. Số nghiệm của phương trình là:
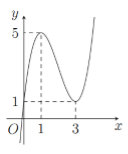
 Xem đáp án
Xem đáp án
Đồ thị hàm số cắt đường thẳng tại 3 điểm phân biệt có 3 nghiệm phân biệt.
Đáp án cần chọn là: D
Câu 3:
Đề thi THPT QG - 2021 - mã 101
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
 Xem đáp án
Xem đáp án
Đồ thị hàm số cắt trục tung
Với thay vào hàm số .
Đáp án cần chọn là: D
Câu 4:
Tọa độ giao điểm của đường thẳng và parabol là:
 Xem đáp án
Xem đáp án
Phương trình hoành độ
Vậy có hai giao điểm là và
Đáp án cần chọn là: C
Câu 5:
Các đồ thị hàm số và có tất cả bao nhiêu điểm chung?
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là:
Như vậy hai đồ thị có 2 giao điểm.
Đáp án cần chọn là: D
Câu 6:
Cho hai đồ thị hàm số và đồ thị hàm số có tất cả bao nhiêu điểm chung?
 Xem đáp án
Xem đáp án
Số giao điểm của hai đồ thị hàm số đã cho là số nghiệm của phương trình:
Vậy hai đồ thị hàm số đã cho có 1 giao điểm duy nhất.
Đáp án cần chọn là: D
Câu 7:
Số giao điểm của hai đồ thị hàm số và là:
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm:
Xét hàm ta có:
Bảng biến thiên:
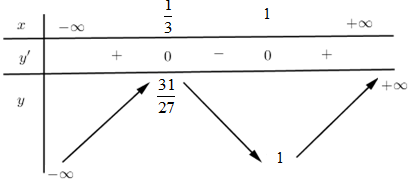
Từ bảng biến thiên ta thấy đường thẳng chỉ cắt đồ thị hàm số tại 1 điểm duy nhất nên hai đồ thị hàm số cắt nhau tại duy nhất 1 điểm.
Đáp án cần chọn là: B
Câu 8:
Cho hàm số bậc ba có bảng biến thiên trong hình dưới:
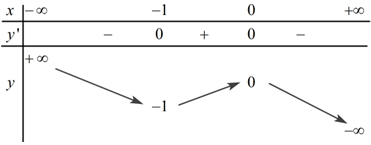
Số nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng
Ta có BBT:
Dựa vào BBT ta thấy đường thẳng cắt đồ thị hàm số tại 3 điểm phân biệt.
⇒ Phương trình có 3 nghiệm phân biệt.
Đáp án cần chọn là: B
Câu 9:
Cho hàm số liên tục trên và có đồ thị như hình vẽ bên. Số nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Ta có
Với thì đường thẳng cắt đồ thị hàm số tại 2 điểm phân biệt.
Với thì đường thẳng cắt đồ thị hàm số tại 2 điẻm phân biệt.
Vậy tổng có tất cả 4 nghiệm phân biệt.
Đáp án cần chọn là: B
Câu 10:
Tìm m để phương trình có nghiệm trên
 Xem đáp án
Xem đáp án
Ta có số nghiệm của phương trình đã cho là số giao điểm của đồ thị (C):
và đường thẳng d:
Xét hàm số (C): có:
⇒ hàm số luôn đồng biến trên
Lại có
Ta có BBT:
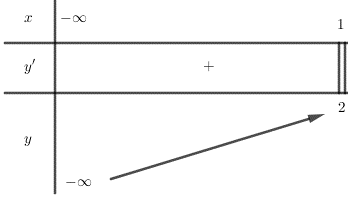
Theo BBT ta thấy pt có nghiệm
Đáp án cần chọn là: A
Câu 11:
Cho hàm số có đồ thị (C).Để đồ thị (C) cắt trục hoành tại ba điểm A,B,C sao cho C là trung điểm của AB thì giá trị của tham số m là:
 Xem đáp án
Xem đáp án
Vì đồ thị của hàm đa thức bậc 3 luôn có tâm đối xứng có hoành độ x0 là nghiệm của phương trình
Vậy đồ thị (C) cắt trục hoành tại ba điểm A,B,C sao cho C là trung điểm AB
⇔C là tâm đối xứng của (C)
Ta có:
Đáp án cần chọn là: A
Câu 12:
Biết đường thẳng cắt đồ thị hàm số tại ba điểm phân biệt. Tất cả các giá trị thực của tham số m là:
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm
Để đường thẳng cắt đồ thị hàm số tại 3 điểm phân biệt thì (∗) phải có hai nghiệm phân biệt khác
Đáp án cần chọn là: A
Câu 13:
Cho hàm số Tập hợp tất cả các giá trị của m để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt có hoành độ âm là:
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:
Để đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt có hoành độ âm thì phương trình (∗) có 2 nghiệm âm phân biệt khác −1
Đáp án cần chọn là: A
Câu 14:
Tìm m để đồ thị hàm số cắt đường thẳng tại ba điểm phân biệt có hoành độ thỏa mãn
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm:
Để hai đồ thị hàm số cắt nhau tại ba điểm phân biệt thì phương trình hoành độ có 3 nghiệm phân biệt
⇔(∗) có 2 nghiệm phân biệt khác 1⇔
Gọi lần lượt là nghiệm của phương trình
Ta có:
Đáp án cần chọn là: A
Câu 15:
Tìm điều kiện của m để đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt.
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm
Đặt ta được phương trình
Để đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt thì phương trình phải có hai nghiệm dương phân biệt
Đáp án cần chọn là: B
Câu 16:
Cho hàm số Các giá trị của tham số m để đồ thị hàm số (1) cắt trục hoành tại 4 điểm phân biệt có hoành độ thoả mãn
 Xem đáp án
Xem đáp án
Đặt
Phương trình có 4 nghiệm phân biệt thỏa mãn có hai nghiệm phân biệt dương thỏa mãn hay
Đáp án cần chọn là: A
Câu 17:
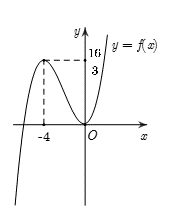
Cho hàm số liên tục trên và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm?
 Xem đáp án
Xem đáp án
Vì nên
Đặt
Phương trình trên có nghiệm khi
Từ đồ thị hàm số ta thấy hàm số f(x) đồng biến trên (0;1)
Nên phương trình với có nghiệm duy nhất khi
Do đó phương trình có nghiệm
có nghiệm với
Mà nên . Vậy có 3 giá trị của m thỏa mãn yêu cầu.
Mình cần đánh giá cho biểu thức này em nhé :
Mục đích đánh giá là để có thể quy đồng sau khi đặt t. Từ đó tìm điều kiện cho t.
Đáp án cần chọn là: D
Câu 18:
Cho hàm số liên tục trên và có bảng biến thiên như sau
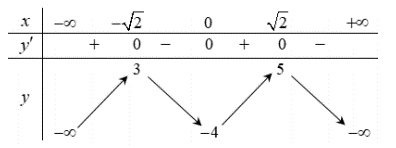
Có bao nhiêu giá trị nguyên của tham số m sao cho phương trình có hai nghiệm
phân biệt trên khoảng ?
 Xem đáp án
Xem đáp án
Ta có mà
Đặt thì
Đưa về bài toán tìm m để phương trình có hai nghiệm phân biệt trên khoảng
Ta có
Từ BBT ta suy ra mà
Nên có 13 giá trị của m thỏa mãn đề bài.
Đáp án cần chọn là: A
Câu 19:
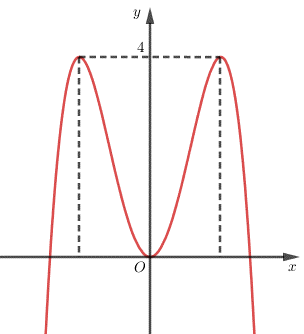
Cho hàm số có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số mm để phương trình có hai nghiệm phân biệt.
 Xem đáp án
Xem đáp án
Phương trình có hai nghiệm phân biệt ⇔ đường thẳng cắt đồ thị hàm số đã cho tại hai điểm phân biệt
Đáp án cần chọn là: B
Câu 20:
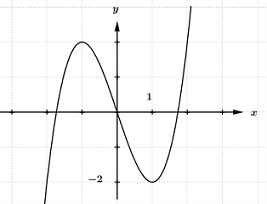
Cho hàm số có đồ thị như hình vẽ. Với các giá trị nào của tham số m thì phương trình có bốn nghiệm phân biệt.
 Xem đáp án
Xem đáp án
Dựa vào đồ thị hàm số ta suy ra được đồ thị hàm số như sau:
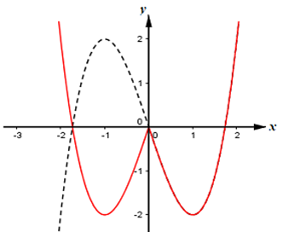
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng song song với trục hoành.
Do đó để phương trình có 4 nghiệm phân biệt thì
Đáp án cần chọn là: C
Câu 21:
Cho hàm số liên tục trên R và có bảng biến thiên như hình vẽ
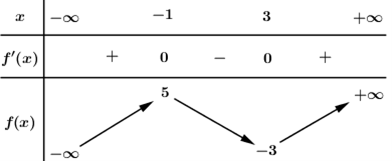
Phương trình có bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Đặt
Dễ thấy với mỗi x chỉ có một x và ngược lại.
Do đó số nghiệm x của phương trình đã cho bằng số nghiệm t của phương trình
Ta có:
Từ bbt ta thấy,
+) Đường thẳng y = 7 cắt đồ thị hàm số tại duy nhất 1 điểm nên (1) có 1 nghiệm.
+) Đường thẳng y = −3 cắt đồ thị hàm số tại 2 điểm nên (2) có 2 nghiệm.
Dễ thấy các nghiệm của (1) và (2) phân biệt.
Vậy phương trình đã cho có tất cả 3 nghiệm.
Đáp án cần chọn là: A
Câu 22:
Cho hàm số liên tục trên và có đồ thị như hình vẽ bên. Số nghiệm của phương trình là:
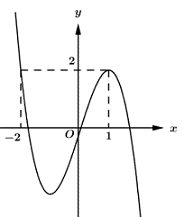
 Xem đáp án
Xem đáp án
Đặt phương trình trở thành
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng y = 2 .
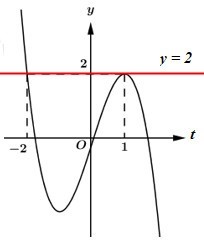
Dựa vào đồ thị hàm số ta thấy
+ Số nghiệm của phương trình (1) là số giao điểm của đồ thị hàm số và đường thẳng y = 0 nên phương trình (1) có 3 nghiệm phân biệt.
+ Số nghiệm của phương trình (2) là số giao điểm của đồ thị hàm số và đường thẳng y = 3 nên phương trình (1) có 1 nghiệm duy nhất.
Vậy phương trình đã cho có tất cả 4 nghiệm.
Đáp án cần chọn là: D
Câu 23:
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn của tham số m để đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt?
 Xem đáp án
Xem đáp án
TXĐ:
Xét phương trình hoành độ giao điểm:
Để để đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt khác 1
Kết hợp điều kiện bài toán ta suy ra
Vậy có 2019 + 2017 = 4036 giá trị của m thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: A
Câu 24:
Cho hàm số . Giá trị của tham số m để đường thẳng cắt tại ba điểm phân biệt sao cho tam giác KBC có diện tích bằng với điểm là:
 Xem đáp án
Xem đáp án
+ Xét phương trình hoành độ giao điểm của đồ thị và đường thẳng ta có:
Để (d) cắt (Cm) tại 3 điểm phân biệt thì phương trình (1) có 2 nghiệm phân biệt khác 0
Gọi là 2 nghiệm phân biệt của phương trình (1)
Khi đó áp dụng định lí Vi-ét ta có:
Ta có:
Phương trình đường thẳng
Vì B,C thuộc đường thẳng (d) nên ta có:
Theo bài ra ta có:
Vậy
Đáp án cần chọn là: C
Câu 25:
Cho hàm số có bảng biến thiên:
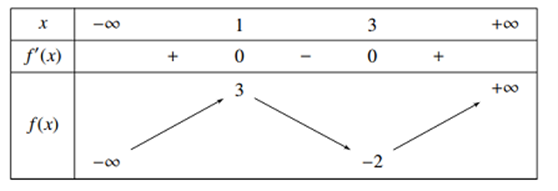
Tìm tất cả các giá trị của mm để bất phương trình vô nghiệm?
 Xem đáp án
Xem đáp án
Đặt ta có:
Bất phương trình vô nghiệm khi và chỉ khi vô nghiệm với mọi
Từ BBT của hàm số ta thấy: nghiệm với khi m > 3.
Vậy m > 3.
Đáp án cần chọn là: D
Câu 26:
Cho hàm số f(x) có bảng biến thiên như sau:
Phương trình có bao nhiêu nghiệm thực?
 Xem đáp án
Xem đáp án
Bước 1: Đặt Đưa phương trình đã cho về phương trình ẩn t
Đặt
Phương trình đã cho trở thành
Bước 2: Biện luận số nghiệm của x
Dựa vào BBT ta thấy đường thẳng cắt đồ thị hàm số tại 3 điểm có hoành độ lớn hơn hoặc bằng −1.
Suy ra phương trình (*) có 3 nghiệm thực t, ứng với mỗi nghiệm t cho 2 nghiệm thực x.
Vậy phương trình đã cho có 6 nghiệm thực.
Câu 27:
 Xem đáp án
Xem đáp án
Bước 1: Đặt quan sát đồ thị tìm nghiệm của phương trình tìm các nghiệm ti.
Ta có :
Đặt ta được
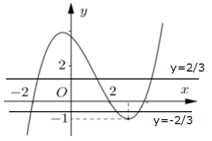
+) Phương trình có ba nghiệm phân biệt trong đó
+) Phương trình có ba nghiệm phân biệt trong đó
Các nghiệm
Bước 2: Khảo sát hàm số suy ra số nghiệm của phương trình
Xét hàm có
BBT :
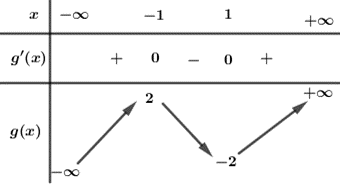
Từ BBT ta thấy :
+) Phương trình có 3 nghiệm phân biệt.
+) Phương trình có 3 nghiệm phân biệt.
+) Phương trình có đúng 1 nghiệm.
+) Phương trình có đúng 1 nghiệm.
+) Phương trình có đúng 1 nghiệm.
+) Phương trình có đúng 1 nghiệm.
Vậy phương trình đã cho có tất cả nghiệm.
Câu 28:
Cho hàm số . Tìm tất cả các giá trị của tham số m sao cho phương trình có 4 nghiệm phân biệt.
 Xem đáp án
Xem đáp án
Số nghiệm của pt số giao điểm của đồ thị hàm số và đường thẳng
Ta có đồ thị hàm số như hình vẽ:
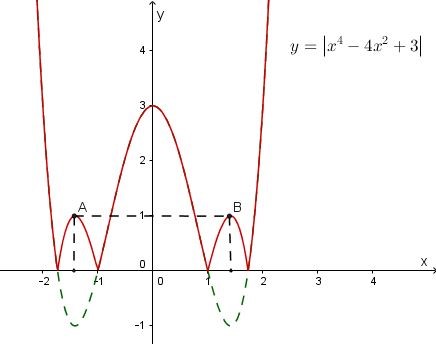
Để pt (∗)(∗) có 4 nghiệm phân biệt thì đường thẳng cắt đồ thị hàm số tại 4 điểm phân biệt.
Quan sát đồ thị ta thấy đường thẳng cắt đồ thị hàm số tại 4 điểm phân biệt
Đáp án cần chọn là: B
Câu 29:
Tìm mm để phương trình có 6 nghiệm phân biệt.
 Xem đáp án
Xem đáp án
Số nghiệm của pt là số giao điểm của đồ thị hàm số và đường thẳng
Ta có đồ thị hàm số
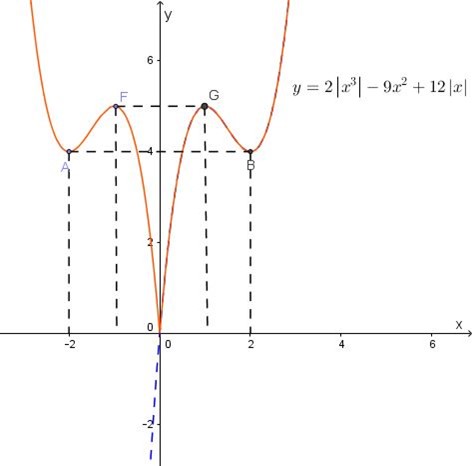
Pt có 6 nghiệm phân biệt khi và chỉ khi đường thẳng cắt đồ thị hàm số tại 6 điểm phân biệt
Đáp án cần chọn là: D
Câu 30:
 Xem đáp án
Xem đáp án
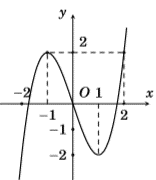
Ta có: khi đó dựa vào đồ thị hàm số ta có
Đặt
Khi đó yêu cầu bài toán trở thành: Tổng tất cả giá trị nguyên của tham số m để phương trình có nghiệm
Dựa vào đồ thị hàm số ta thấy với thì do đó phương trình có nghiệm
Mà
Vậy tổng các giá trị của m thỏa mãn là
Đáp án cần chọn là: D
Câu 31:
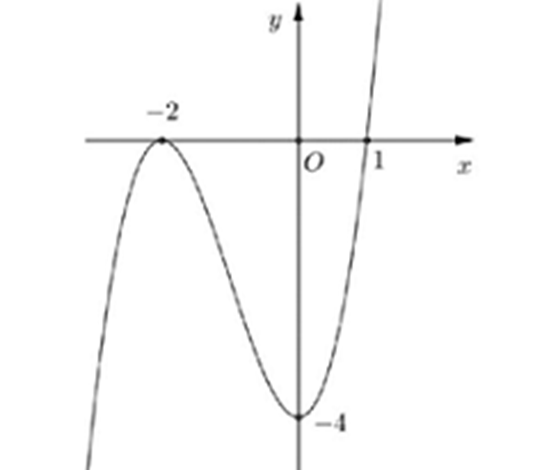
Có tất cả bao nhiêu giá trị nguyên của tham số để phương trình có 6 nghiệm phân biệt
 Xem đáp án
Xem đáp án
Ta có
Dựng đồ thị hàm số ta được:
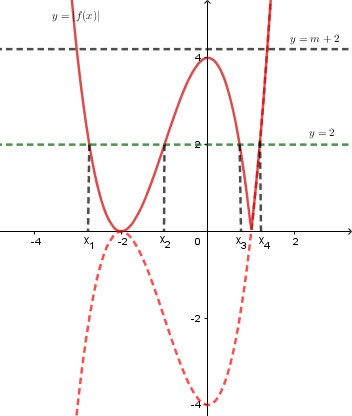
Dễ thấy phương trình có 4 nghiệm phân biệt nên để phương trình đã cho có 6 nghiệm phân biệt thì phương trình phải có 2 nghiệm phân biệt khác các nghiệm trên.
Do đó đường thẳng cắt đồ thị hàm số tại 2 điểm phân biệt.
Từ hình vẽ ta có
Mà và nên
Vậy có 3 giá trị thỏa mãn.
Đáp án cần chọn là: C
Câu 32:
Cho hàm số liên tục trên và có bảng biến thiên như hình vẽ.
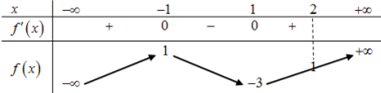
Có bao nhiêu giá trị nguyên của tham số m để phương trình có đúng 2 nghiệm trên
 Xem đáp án
Xem đáp án
Ta có:
Phương trình (1) vô nghiệm.
Phương trình (2)
Dựa vào BBT trên để phương trình có đúng 2 nghiệm thì
Mà Vậy có 5 giá trị của m thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: D
Câu 33:
Cho hàm số liên tục trên có bảng biến thiên như hình vẽ:
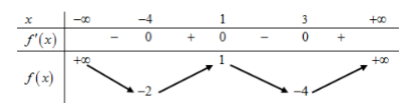
Số nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Ta có:
Tiếp tục dựa vào BBT ta có:
- Phương trình (1.1) có 0 nghiệm.
- Phương trình (1.2) có 2 nghiệm phân biệt.
- Phương trình (2.1) có 1 nghiệm.
- Phương trình (2.2) có 2 nghiệm phân biệt.
- Phương trình (2.3) có 2 nghiệm phân biệt.
Rõ ràng 7 nghiệm trên là phân biệt.
Vậy phương trình có 7 nghiệm phân biệt.
Đáp án cần chọn là: C
