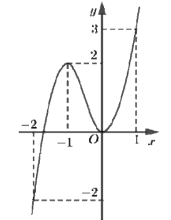
Cho hàm số y=f(x)) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y=f(x) trên đoạn \[\left[ { - 2;2} \right]\]
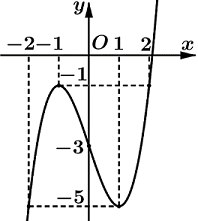
A.m=−5,M=−1.
B.m=−1,M=0.
C.m=−2,M=2.
D.m=−5,M=0.
 Giải bởi Vietjack
Giải bởi Vietjack
Dựa vào đồ thị hàm số ta có:\(\left\{ {\begin{array}{*{20}{c}}{m = \mathop {min}\limits_{[ - 2;2]} f(x) = - 5}\\{M = \mathop {max}\limits_{[ - 2;2]} f(x) = - 1}\end{array}} \right.\)
Đáp án cần chọn là: A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Người ta cần chế tạo các món quà lưu niệm bằng đồng có dạng khối chóp tứ giác đều, được mạ vàng bốn mặt bên và có thể tích bằng 16cm3. Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu cm2? (Kết quả làm tròn đến hàng đơn vị.)
Cho hàm số \[y = {x^3} - 3m{x^2} + 6\], giá trị nhỏ nhất của hàm số trên \[\left[ {0;3} \right]\;\]bằng 2 khi:
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=sinx trên đoạn \[[ - \frac{\pi }{2}; - \frac{\pi }{3}]\] lần lượt là
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = f(1 - 2cosx)\] trên \[\left[ {0;\frac{{3\pi }}{2}} \right].\]Giá trị của M+m bằng
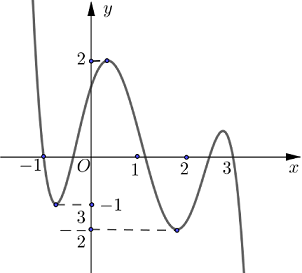
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) có đồ thị \[y = f\prime (x)\;\] như hình vẽ. Đặt \[g(x) = 2f(x) - {x^2}\]. Khi đó giá trị lớn nhất của hàm số g(x) trên đoạn \[\left[ { - 2;4} \right]\;\]là:
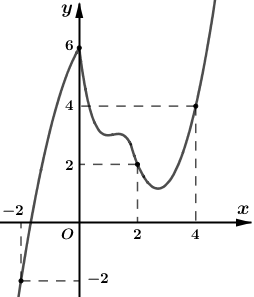
Cho hàm số f(x) xác định và liên tục trên R, có \[\mathop {\lim }\limits_{x \to + \infty } = + \infty ;\mathop {\lim }\limits_{x \to - \infty } = - \infty \] , khi đó:
Cho biết GTLN của hàm số f(x) trên \[\left[ {1;3} \right]\;\]là M=−2. Chọn khẳng định đúng:
Giá trị nhỏ nhất của hàm số \[y = 2x + \cos x\] trên đoạn \[\left[ {0;1} \right]\;\]là :
Cho hàm số f(x) xác định trên \[\left[ {0;2} \right]\;\]và có GTNN trên đoạn đó bằng 5. Chọn kết luận đúng:
Cho hàm số y=f(x) có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
Cho hàm số \[y = x + \frac{1}{x}.\] Giá trị nhỏ nhất của hàm số trên khoảng \[\left( {0; + \infty } \right)\;\]là:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ, chọn kết luận đúng:
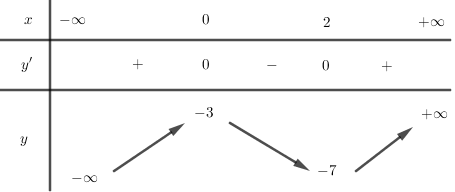
Có bao nhiêu số nguyên \[m \in [ - 5;5]\;\] để \[\mathop {min}\limits_{\left[ {1;3} \right]} \mid {x^3} - 3{x^2} + m\mid \ge 2.\]
Gọi giá trị lớn nhất và nhỏ nhất của hàm số \[y = {x^4} + 2{x^2} - 1\;\] trên đoạn \[\left[ { - 1;2} \right]\;\]lần lượt là M và m. Khi đó giá trị của M.m là:
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình dưới. Gọi a,A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của f(x+1) trên đoạn \[\left[ { - 1;0} \right].\;\]Giá trị a+A bằng: