Tìm a biết \(I = \int\limits_{ - 1}^2 {\frac{{{e^x}dx}}{{2 + {e^x}}}} = \ln \frac{{ae + {e^3}}}{{ae + b}}\) với a,bb là các số nguyên dương.
A.\[a = 1\]
B. \[a = - \frac{1}{3}\]
C. \[a = 2\]
D. \[a = --2\]
Giải bởi Vietjack
Đặt \[t = {e^x} \Rightarrow dt = {e^x}dx\]
Đổi cận:\(\left\{ {\begin{array}{*{20}{c}}{x = - 1 \Rightarrow t = {e^{ - 1}}}\\{x = 2 \Rightarrow t = {e^2}}\end{array}} \right.\)
Khi đó
\(\begin{array}{l}I = \int\limits_{{e^{ - 1}}}^{{e^2}} {\frac{{dt}}{{t + 2}}} = ln|t + 2|\left| {_{{e^{ - 1}}}^{{e^2}}} \right. = ln({e^2} + 2) - ln({e^{ - 1}} + 2) = ln\frac{{{e^2} + 2}}{{{e^{ - 1}} + 2}}\\ = \ln \frac{{{e^2} + 2}}{{\frac{1}{e} + 2}} = \ln \frac{{2e + {e^3}}}{{2e + 1}} = \ln \frac{{ae + {e^3}}}{{ae + b}}\end{array}\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{ae + {e^3} = 2e + {e^3}}\\{ae + b = 2e + 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b = 1}\end{array}} \right.\)
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Đổi biến \[x = 4\sin t\] của tích phân \(I = \int\limits_0^{\sqrt 8 } {\sqrt {16 - {x^2}} } \) ta được:
Cho hàm số f(x) liên tục trên R và \[\mathop \smallint \limits_{ - 2}^4 f(x)dx = 2\] . Mệnh đề nào sau đây là sai?
Cho tích phân \[I = \mathop \smallint \limits_0^{\frac{\pi }{2}} \sin x\sqrt {8 + \cos x} dx\] Đặt \[u = 8 + cosx\] thì kết quả nào sau đây là đúng?
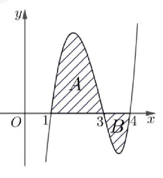
Cho hàm số y=f(x) có đồ thị như hình vẽ. Biết các miền A và B có diện tích lần lượt là 4 và 1. Tính \[I = \mathop \smallint \limits_1^2 4xf\left( {{x^2}} \right)dx\]
Cho tích phân \[I = \mathop \smallint \limits_1^{\sqrt 3 } \frac{{\sqrt {1 + {x^2}} }}{{{x^2}}}dx\]. Nếu đổi biến số \[t = \frac{{\sqrt {{x^2} + 1} }}{x}\;\] thì:
Biết \[\mathop \smallint \limits_0^{\frac{\pi }{2}} \frac{{3\sin x + \cos x}}{{2\sin x + 3\cos x}}dx = - \frac{7}{{13}}\ln 2 + b\ln 3 + c\pi \,\,\left( {b,c \in \mathbb{Q}} \right).\]. Tính \(\frac{b}{c}\).
Cho \[\mathop \smallint \nolimits_0^4 f(x)dx = - 1\], tính \(I = \mathop \smallint \limits_0^1 f(4x)dx\):
Hàm số y=f(x) có nguyên hàm trên (a;b) đồng thời thỏa mãn f(a)=f(b). Lựa chọn phương án đúng:
Tính tích phân \[I = \mathop \smallint \limits_0^\pi {\cos ^3}x\sin xdx\]
Đặt \[\cos x = t \Rightarrow - \sin xdx = dt \Rightarrow \sin xdx = - dt\]
Đổi cận:\(\left\{ {\begin{array}{*{20}{c}}{x = 0 \Rightarrow t = 1}\\{x = \pi \Rightarrow t = - 1}\end{array}} \right.\)
\( \Rightarrow I = - \int\limits_1^{ - 1} {{t^3}dt = } \int\limits_{ - 1}^1 {{t^3}dt = \frac{{{t^4}}}{4}} \left| {_{ - 1}^1} \right. = \frac{1}{4} - \frac{1}{4} = 0\)
Cho \[I = \mathop \smallint \limits_1^e \frac{{\sqrt {1 + 3\ln x} }}{x}dx\] và \[t = \sqrt {1 + 3lnx} \;\]. Chọn khẳng định sai trong các khẳng định sau:
Cho hàm số f(x) liên tục trên đoạn \[\left[ {0;1} \right]\;\]và \[\mathop \smallint \limits_0^{\frac{\pi }{2}} f\left( {\sin x} \right)dx = 5\] Tính \[I = \mathop \smallint \limits_0^\pi xf\left( {\sin x} \right)dx\]
Cho hàm số f(x) liên tục trên \[\left[ { - 1;2} \right]\]và thỏa mãn điều kiện \[f\left( x \right) = \sqrt {x + 2} + xf\left( {3 - {x^2}} \right)\] Tính tích phân \[\mathop \smallint \limits_{ - 1}^2 f\left( x \right)dx\]
Với mỗi số k, đặt \[{I_k} = \int\limits_{ - \sqrt k }^{\sqrt k } {\sqrt {k - {x^2}} } dx\]. Khi đó \[{I_1} + {I_2} + {I_3} + ... + {I_{12}}\;\] bằng:
Cho y=f(x) là hàm số lẻ và liên tục trên \[\left[ { - a;a} \right].\]Chọn kết luận đúng:
Cho \[2\sqrt 3 m - \mathop \smallint \limits_0^1 \frac{{4{x^3}}}{{{{\left( {{x^4} + 2} \right)}^2}}}dx = 0\]. Khi đó \[144{m^2} - 1\;\]bằng:
