Cho hàm số f(x) liên tục trên $\mathbb{R}$ và $\mathop \smallint \limits_1^9 \frac{{f\left( {\sqrt x } \right)}}{{\sqrt x }}{\rm{d}}x = 4,\mathop \smallint \limits_0^{\frac{\pi }{2}} f\left( {\sin x} \right)\cos x{\rm{d}}x = 2$. Tính tích phân $I = \mathop \smallint \limits_0^3 f\left( x \right){\rm{d}}x$

Đổi biến $x = 4\sin t$ của tích phân $I = \int\limits_0^{\sqrt 8 } {\sqrt {16 - {x^2}} }$ ta được:

Cho tích phân $I = \mathop \smallint \limits_1^{\sqrt 3 } \frac{{\sqrt {1 + {x^2}} }}{{{x^2}}}dx$. Nếu đổi biến số $t = \frac{{\sqrt {{x^2} + 1} }}{x}\;$ thì:

Biết $\mathop \smallint \limits_0^{\frac{\pi }{2}} \frac{{3\sin x + \cos x}}{{2\sin x + 3\cos x}}dx = - \frac{7}{{13}}\ln 2 + b\ln 3 + c\pi \,\,\left( {b,c \in \mathbb{Q}} \right).$. Tính $\frac{b}{c}$.

Cho hàm số f(x) liên tục trên R  và $\mathop \smallint \limits_{ - 2}^4 f(x)dx = 2$ . Mệnh đề nào sau đây là sai?

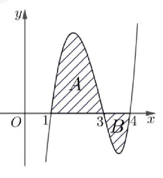
Cho hàm số y=f(x) có đồ thị như hình vẽ. Biết các miền A và B có diện tích lần lượt là 4 và 1. Tính $I = \mathop \smallint \limits_1^2 4xf\left( {{x^2}} \right)dx$

Cho tích phân $I = \mathop \smallint \limits_0^{\frac{\pi }{2}} \sin x\sqrt {8 + \cos x} dx$ Đặt $u = 8 + cosx$ thì kết quả nào sau đây là đúng?

Cho $\mathop \smallint \nolimits_0^4 f(x)dx = - 1$, tính $I = \mathop \smallint \limits_0^1 f(4x)dx$:

Cho $I = \mathop \smallint \limits_1^e \frac{{\sqrt {1 + 3\ln x} }}{x}dx$ và $t = \sqrt {1 + 3lnx} \;$. Chọn khẳng định sai trong các khẳng định sau:

Hàm số y=f(x) có nguyên hàm trên (a;b)  đồng thời thỏa mãn f(a)=f(b). Lựa chọn phương án đúng:

Tính tích phân $I = \mathop \smallint \limits_0^\pi {\cos ^3}x\sin xdx$

Đặt $\cos x = t \Rightarrow - \sin xdx = dt \Rightarrow \sin xdx = - dt$

Đổi cận:$\left\{ {\begin{array}{*{20}{c}}{x = 0 \Rightarrow t = 1}\\{x = \pi \Rightarrow t = - 1}\end{array}} \right.$

$\Rightarrow I = - \int\limits_1^{ - 1} {{t^3}dt = } \int\limits_{ - 1}^1 {{t^3}dt = \frac{{{t^4}}}{4}} \left| {_{ - 1}^1} \right. = \frac{1}{4} - \frac{1}{4} = 0$

Cho hàm số f(x) liên tục trên đoạn $\left[ {0;1} \right]\;$và $\mathop \smallint \limits_0^{\frac{\pi }{2}} f\left( {\sin x} \right)dx = 5$ Tính $I = \mathop \smallint \limits_0^\pi xf\left( {\sin x} \right)dx$

Với mỗi số k, đặt ${I_k} = \int\limits_{ - \sqrt k }^{\sqrt k } {\sqrt {k - {x^2}} } dx$. Khi đó ${I_1} + {I_2} + {I_3} + ... + {I_{12}}\;$ bằng:

Cho y=f(x) là hàm số lẻ và liên tục trên $\left[ { - a;a} \right].$Chọn kết luận đúng:

Cho hàm số f(x) liên tục trên $\left[ { - 1;2} \right]$và thỏa mãn điều kiện $f\left( x \right) = \sqrt {x + 2} + xf\left( {3 - {x^2}} \right)$ Tính tích phân $\mathop \smallint \limits_{ - 1}^2 f\left( x \right)dx$

Cho $\mathop \smallint \limits_0^1 f\left( x \right)dx = 1.$Tính $I = \mathop \smallint \limits_0^{\frac{\pi }{4}} \left( {2{{\sin }^2}x - 1} \right)f\left( {\sin 2x} \right)dx$