Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác cân tại A. \(AB = AC = 2a,\widehat {CAB} = {120^0}\). Mặt phẳng \[(AB\prime C\prime )\] tạo với đáy một góc 600. Thể tích khối lăng trụ là:
A.\[2{a^3}\]
B. \[\frac{{3{a^3}}}{8}\]
C. \[\frac{{{a^3}}}{3}\]
D. \[3{a^3}\]
Giải bởi Vietjack
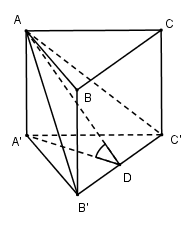
Gọi D là trung điểm của B′C′. Vì tam giác A′B′C′ cân tại A′ nên \[A'D \bot B'C'\] (trung tuyến đồng thời là đường cao).
Vì ABC.A′B′C′ là hình lăng trụ đứng nên\[AA' \bot (A'B'C')\]
Ta có:\(\left. {\begin{array}{*{20}{c}}{A\prime D \bot B\prime C\prime }\\{AA\prime \bot B\prime C\prime }\end{array}} \right\} \Rightarrow B\prime C\prime \bot (AA\prime D) \Rightarrow B\prime C\prime \bot AD\)
\(\left. {\begin{array}{*{20}{c}}{(AB\prime C\prime ) \cap (A\prime B\prime C\prime ) = B\prime C'}\\{(AB\prime C\prime ) \supset AD \bot B\prime C\prime }\\{(A\prime B\prime C\prime ) \supset A\prime D \bot B\prime C\prime }\end{array}} \right\} \Rightarrow ((AB\prime \widehat {C\prime );(A\prime }B\prime C\prime )) = (A\widehat {D;A\prime }D) = \widehat {ADA}\prime = {60^0}\)
Vì tam giác A′B′C′ cân tại A′ nên\[\widehat {DA'C'} = \frac{1}{2}\widehat {B'A'C'} = {60^0}\] (trung tuyến đồng thời là phân giác)
Xét tam giác vuông A′D′C′ có: \[A'D = A'C'.cos60 = 2a.\frac{1}{2} = a\]
Xét tam giác vuông AA′D có:\[AA' = A'D.\tan 60 = a.\sqrt 3 \]
\[{S_{ABC}} = \frac{1}{2}AB.AC.\sin \widehat {BAC} = \frac{1}{2}.2a.2a.\frac{{\sqrt 3 }}{2} = {a^2}\sqrt 3 \]
Vậy\[{V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = a\sqrt 3 .{a^2}\sqrt 3 = 3{a^3}\]
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Công thức tính thể tích lăng trụ có diện tích đáy SS và chiều cao hh là:
Cho hình lăng trụ ABC.A′B′C′ có AB=2a,AC=a,\(AA' = \frac{{a\sqrt {10} }}{2},\widehat {BAC} = {120^0}\). Hình chiếu vuông góc của C′ lên (ABC) là trung điểm của cạnh BC. Tính thể tích khối lăng trụ ABC.A′B′C′ theo a?
Lăng trụ đứng tứ giác có đáy là hình thoi mà các đường chéo là 6cm và 8cm, biết rằng chu vi đáy bằng 2 lần chiều cao lăng trụ. Tính thể tích khối lăng trụ
Đề thi THPT QG - 2021 - mã 101
Cho khối hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông, BD=2a, góc giữa hai mặt phẳng \[(A\prime BD)\;\]và (ABCD) bằng 300. Thể tích của khối hộp chữ nhật đã cho bằng
Cho lăng trụ xiên tam giác ABC.A′B′C′ có đáy ABC là tam giác đều cạnh a, biết cạnh bên là \(a\sqrt 3 \) và hợp với đáy ABC một góc 600. Thể tích khối lăng trụ là:
Thể tích khối hộp chữ nhật có diện tích đáy S và độ dài cạnh bên a là:
Cho khối lăng trụ tam giác ABC.A′B′C′ mà mặt bên ABB′A′ có diện tích bằng 4. Khoảng cách giữa CC′ và mặt phẳng (ABB′A′) bằng 7. Thể tích khối lăng trụ là:
Cho khối lăng trụ tam giác ABC.A′B′C′ có thể tích V. Trên đáy A′B′C′ lấy điểm M bất kì. Thể tích khối chóp M.ABC tính theo V bằng:
Cho khối lăng trụ ABC.A′B′C′. Gọi E là trọng tâm tam giác A′B′C′ và F là trung điểm BC. Gọi V1 là thể tích khối chóp B′.EAF và V2 là thể tích khối lăng trụ ABC.A′B′C′. Khi đó \[\frac{{{V_1}}}{{{V_2}}}\] có giá trị bằng
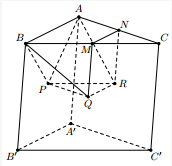
Cho hình lăng trụ tam giác ABC.A′B′C′ có diện tích đáy bằng 12 và chiều cao bằng 66. Gọi M,N lần lượt là trung điểm của CB,CA và P,Q,R lần lượt là tâm các hình bình hành ABB′A′, BCC′B′, CAA′C′. Thể tích của khối đa diện PQRABMN bằng:
\[\]Đề thi THPT QG – 2021 lần 1– mã 104
Thể tích của khối lập phương cạnh 2a bằng:
Đáy của hình lăng trụ đứng tam giác ABC.A′B′C′ là tam giác đều cạnh a=4 và biết diện tích tam giác A′BC bằng 8 . Tính thể tích khối lăng trụ?
Cho hình lăng trụ ABCD.A′B′C′D′ có đáy ABCD là hình thoi cạnh a và góc \(\widehat A = {60^0}\). Chân đường cao hạ từ B′ xuống (ABCD) trùng với giao điểm 2 đường chéo, biết BB′=a . Thể tích khối lăng trụ là:
Cho hình lăng trụ ABCD.A′B′C′D′ có đáy ABCD là hình vuông cạnh bằng a. Hình chiếu vuông góc của điểm A′ trên mặt phẳng (ABCD) là trung điểm I của cạnh AB. Biết A′C tạo với mặt phẳng đáy một góc α với \[tan\alpha = \frac{2}{{\sqrt 5 }}\]. Thể tích khối chóp A′.ICD là:
