Công thức tính thể tích khối trụ có bán kính r và chiều cao h là:
A.\[V = \frac{1}{3}\pi {r^2}h\]
B. \[V = \pi {r^2}h\]
C. \[V = \pi {h^2}r\]
D. \[V = 2\pi {r^2}h\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chữ nhật ABCD có AB = 3, BC = 4. Gọi V1,V2 lần lượt là thể tích của các khối trụ sinh ra khi quay hình chữ nhật quanh trục AB và BC. Khi đó tỉ số\(\frac{{{V_2}}}{{{V_2}}}\) bằng:
Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2 . Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần Stp của hình trụ đó.
Tính thể tích V của khối trụ ngoại tiếp hình lập phương có cạnh bằng a.
Nếu cắt mặt trụ tròn xoay bởi một mặt phẳng tạo với trục một góc \[\alpha ({0^0} < \alpha < {90^0})\;\] thì ta được:
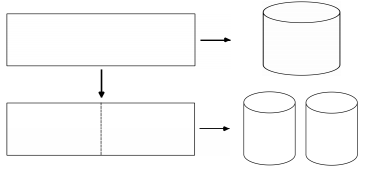
Từ một tấm tôn hình chữ nhật kích thước 50cm×240cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):
- Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
- Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V1 là thể tích của thùng gò được theo cách 1 và V2 là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\)
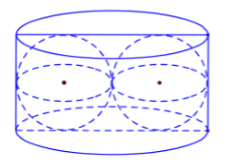
Người ta xếp hai quả cầu có cùng bán kính r vào một chiếc hộp hình trụ sao cho các quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp xúc với đường sinh của hình trụ (tham khảo hình vẽ). Biết thể tích khối trụ là 120cm3, thể tích của mỗi khối cầu bằng
Một sợi dây (không co giãn) được quấn đối xứng đúng 10 vòng quanh một ống trụ tròn đều có bán kính \(R = \frac{2}{\pi }cm\) (như hình vẽ).
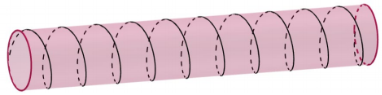
Biết rằng sợi dây có chiều dài 50 cm. Hãy tính diện tích xung quanh của ống trụ đó.
D.120 cm2
Khi quay hình chữ nhật MNPQ quanh đường thẳng AB với A,B lần lượt là trung điểm của MN,PQ ta được một hình trụ có đường kính đáy:
Một hình trụ có diện tích xung quanh là \[16\pi \], thiết diện qua trục là hình vuông. Một mặt phẳng \[(\alpha )\;\]song song với trục, cắt hình trụ theo thiết diện là ABB′A′, biết một cạnh thiết diện là một dây của đường tròn đáy hình trụ và căng một cung 1200. Chu vi tứ giác ABB′A′ bằng:
Cho hình trụ có chiều cao bằng bán kính đáy và bằng 5cm. Mặt phẳng \[(\alpha )\;\]song song với trục, cắt hình trụ theo một thiết diện có chu vi bằng 26cm. Khoảng cách từ \[(\alpha )\;\]đến trục của hình trụ bằng:
Cho hình chữ nhật ABCD, khi quay hình chữ nhật quanh cạnh AD thì CD được gọi là:
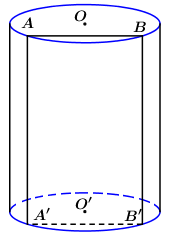
Cho hình trụ có trục \[\Delta \] và bán kính R. Khi cắt hình trụ bởi mặt phẳng \[(\alpha )\;\]song song với \[\Delta \] và cách \[\Delta \] một khoảng \[d(\Delta ;(\alpha )) = k < R\;\] thì ta được thiết diện là:
Cho hình trụ có bán kính đáy bằng a. Cắt hình trụ bởi một mặt phẳng song song với trục của hình trụ và cách trục của hình trụ một khoảng bằng \(\frac{a}{2}\) ta được thiết diện là một hình vuông. Tính thể tích khối trụ.
Cho hai đường thẳng d và \[\Delta \], điều kiện nào sau đây của d và \[\Delta \] thì khi quay d quanh \[\Delta \] ta được một mặt trụ?