Giải bởi Vietjack
Phương pháp:
+ Định luật Faraday thứ nhất: Khối lượng vật chất được giải phóng ở điện cực của bình điện phân tỉ lệ thuận với điện lượng chạy qua bình: \[m = kq\]
+ Định luật Faraday thứ hai: Đương lượng điện hóa k của một nguyên tố tỉ lệ với đương lượng gam \[\frac{A}{n}\] của nguyên tố đó. Hệ số tỉ lệ là \[\frac{1}{F},\] trong đó F gọi là hằng số Fa-ra-day: \[k = \frac{1}{F} \cdot \frac{A}{n}\]
Kết hợp hai định luật: \[m = \frac{1}{F} \cdot \frac{A}{n} \cdot It\]
Cách giải:
Khối lượng của chất giải phóng ở điện cực được tính bằng công thức: \[m = \frac{1}{F} \cdot \frac{A}{n} \cdot It\]
Mà đương lượng điện hóa \[k = \frac{1}{F} \cdot \frac{A}{n} \Rightarrow m = k.It \Rightarrow k = \frac{m}{{I.t}}\]
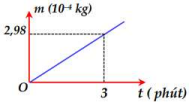
Từ đồ thị ta có: \[t = 3phut = 180s \Rightarrow m = {2,98.10^{ - 4}}kg\]
\[ \Rightarrow k = \frac{m}{{I.t}} = \frac{{{{2,98.10}^{ - 4}}}}{{5.180}} = {3,31.10^{ - 7}}(Kg{\rm{/}}C)\]
Chọn A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
