Cho hình vẽ dưới đây:
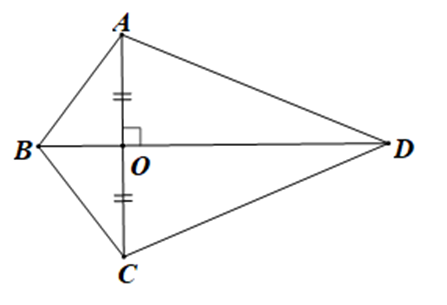
Số cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh là:
A. 1;
B. 2;
C. 3;
D. 4.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
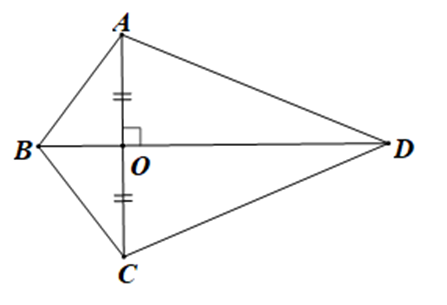
+ Xét tam giác ABO và tam giác CBO có:
AO = CO, \(\widehat {AOB} = \widehat {COB}\left( { = 90^\circ } \right),\) BO là cạnh chung
Do đó DABO = DCBO (c.g.c)
+ Xét DAOD và DCOD có:
AO = CO, \(\widehat {AOD} = \widehat {COD}\left( { = 90^\circ } \right),\) OD là cạnh chung
Do đó D AOD = DCOD (c.g.c)
+ Vì DABO = DCBO (chứng minh trên)
Nên (hai góc tương ứng) và AB = CB (hai cạnh tương ứng)
Xét DABD và DCBD có:
AB = CB (chứng minh trên);
(do )
BD là cạnh chung
Do đó DABD = DCBD (c.g.c)
Vậy có 3 cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho góc xOy khác góc bẹt, gọi Ot là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia đối của tia Ot lấy điểm C tuỳ ý. Chọn phát biểu đúng:
Cho góc nhọn xOy và một điểm A nằm trong góc đó. Kẻ AH ^ Ox tại H và AK ^ Oy tại K. Kéo dài AH một đoạn HB = AH và kéo dài AK một đoạn KC = AK. Nối OA, OB, OC. Chọn phát biểu đúng:
Cho hình vẽ dưới đây:
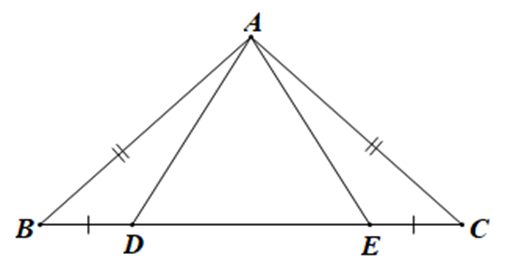
Biết AB = AC, BD = EC, . Xét các khẳng định sau:
(1) DABD = DACE;
(2) DABE = DACD.
Chọn câu đúng:
Cho tam giác BAC và tam giác MNP có BA = MN, CA = MP. Phát biểu nào sau đây là đúng:
Cho tam giác ABC và tam giác DEG có: AB = DE, \(\widehat {ABC} = \widehat {DEG}.\) Điều kiện để DABC = DDEG theo trường hợp cạnh – góc – cạnh là:
Cho DABC và DMNP có AB = NP, \(\widehat B = \widehat N = 55^\circ ,\) BC = NM. Biết \(\widehat A = 50^\circ ,\) số đo góc P là:
Cho hình vuông ABCD, trên cạnh AB lấy điểm M, trên cạnh BC lấy điểm N và trên cạnh DC lấy điểm P sao cho AM = BN = CP. Số đo góc MNP là:
Cho hình vẽ sau:
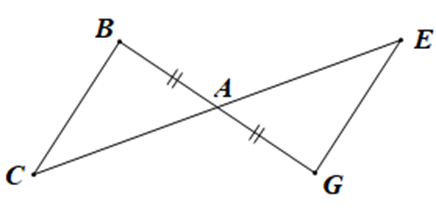
Điều kiện để DABC = DAGE theo trường hợp cạnh – góc – cạnh là:
Cho tam giác ABC có AB = AC = BC, phân giác BD và CE cắt nhau tại O. Chọn phát biểu sai: