Giải bởi Vietjack
Ta có định lý: Tổng bốn góc trong một tứ giác bằng 360º.
+ Hình 5a: Áp dụng định lý trong tứ giác ABCD ta có:
x + 110º + 120º + 80º = 360º
⇒ x = 360º – 110º – 120º – 80º = 50º
+ Hình 5b:Dựa vào hình vẽ ta có: 
Áp dụng định lý trong tứ giác EFGH ta có:
x + 90º + 90º + 90º = 360º
⇒ x = 360º – 90º – 90º – 90º = 90º.
+ Hình 5c:Dựa vào hình vẽ ta có:
Áp dụng định lý trong tứ giác ABDE ta có:
x + 90º + 65º + 90º = 360º
⇒ x = 360º – 90º – 65º – 90º = 115º
+ Hình 5d:
kề bù với góc 60º ⇒ 
kề bù với góc 105º ⇒ 
là góc vuông ⇒ 
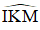
Áp dụng định lý trong tứ giác IKMN ta có:
x + 90º + 120º + 75º = 360º
⇒ x = 360º – 90º – 120º – 75º = 75º
+ Hình 6a: Áp dụng định lý trong tứ giác PQRS ta có:
x + x + 65º + 95º = 360º
⇒ 2x + 160º = 360º
⇒ 2x = 200º
⇒ x = 100º
+ Hình 6b: Áp dụng định lý trong tứ giác MNPQ ta có:
x + 2x + 3x + 4x = 360º
⇒ 10x = 360º
⇒ x = 36º.
Kiến thức áp dụng
Định lý: Tổng bốn góc trong một tứ giác bằng 360º.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.
a) Tính các góc ngoài của tứ giác ở hình 7a.
b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):
c) Có nhận xét gì về tổng các góc ngoài của tứ giác?
a) Nhắc lại định lý về tổng ba góc của một tam giác
b) Vẽ tứ giác ABCD tùy ý. Dựa vào định lý về tổng ba góc của một tam giác, hãy tính tổng A + B + C + D
Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều".
a) Chứng minh rằng AC là đường trung trực của BD.
b) Tính B̂,D̂ biết rằng  = 100º, Ĉ = 60º
Đố. Đố em tìm thấy vị trí của "kho báu" trên hình 11, biết rằng kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3; 2), B(2; 7), C(6; 8), D(8; 5).
Quan sát tứ giác ABCD ở hình 3 rồi điền vào chỗ trống:
a) Hai đỉnh kề nhau: A và B, …
Hai đỉnh đối nhau: A và C, …
b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, …
c) Hai cạnh kề nhau: AB và BC, …
Hai cạnh đối nhau: AB và CD, …
d) Góc: , …
Hai góc đối nhau: và , …
e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, …
Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, …
Trong các tứ giác ở hình 1, tứ giác nào luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác ?
Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ giác ở hình 9, hình 10 vào vở.
