Cho hình vẽ, biết rằng Oz, Ot lần lượt là tia phân giác của \(\widehat {{\rm{yOu}}}\)và \(\widehat {{\rm{zOu}}}\) và \(\widehat {tOu} = a^\circ .\)
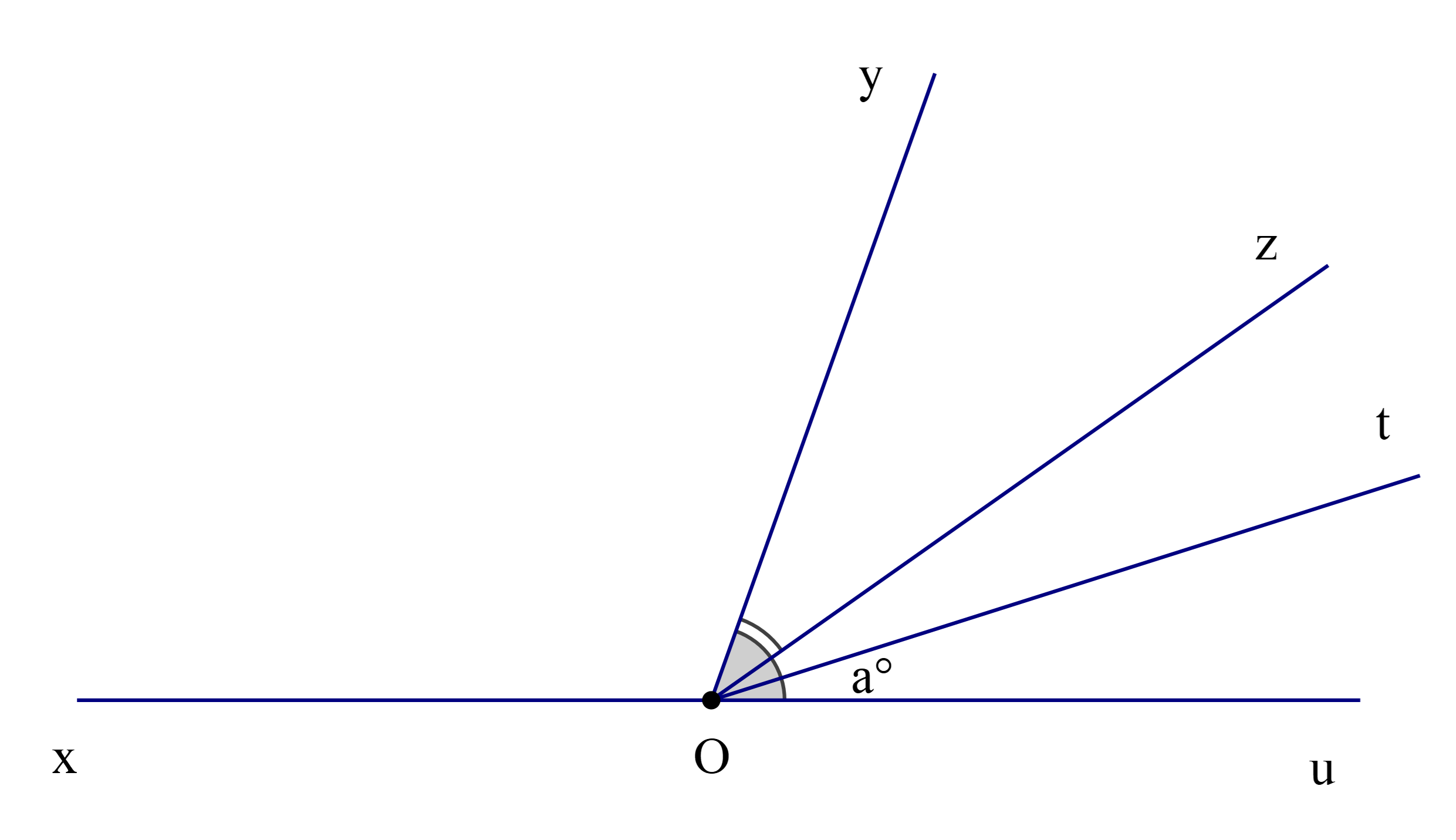
Chọn khẳng định đúng:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Theo bài ra ta có Ot là tia phân giác của \(\widehat {zOu}\)
Suy ra \(\widehat {{\rm{zOt}}} = \widehat {{\rm{tOu}}} = a^\circ \) (tính chất tia phân giác của một góc) (1)
Mà \(\widehat {{\rm{zOt}}} + \widehat {{\rm{tOu}}} = \widehat {{\rm{zOu}}}\) (hai góc kề nhau) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{zOt}}} = \widehat {{\rm{tOu}}} = \frac{{\widehat {{\rm{zOu}}}}}{2}\)
Do đó \(\widehat {zOu} = 2\widehat {{\rm{tOu}}} = 2a^\circ \)
Ta lại có Oz là tia phân giác của \(\widehat {{\rm{yOu}}}\)
Suy ra \(\widehat {{\rm{yOz}}} = \widehat {{\rm{zOu}}}\) (tính chất tia phân giác của một góc) (3)
Mà \(\widehat {{\rm{yOz}}} + \widehat {{\rm{zOu}}} = \widehat {{\rm{yOu}}}\) (hai góc kề nhau) (4)
Từ (3) và (4) suy ra \(\widehat {{\rm{yOz}}} = \widehat {{\rm{zOu}}} = \frac{{\widehat {{\rm{yOu}}}}}{2}\)
Do đó \(\widehat {{\rm{yOu}}} = 2\widehat {{\rm{zOu}}}\)
Mà \(\widehat {{\rm{zOu}}} = 2a^\circ \)
Do đó \(\widehat {{\rm{yOu}}} = 2\widehat {{\rm{zOu}}} = 2.2a^\circ = 4a^\circ \)
Ta có \(\widehat {{\rm{xOy}}} + \widehat {yOu} = 180^\circ \) (hai góc kề bù)
Hay \(\widehat {{\rm{xOy}}} = 180^\circ - \widehat {{\rm{yOu}}}\)
Suy ra \(\widehat {{\rm{xOy}}} = 180^\circ - 4a^\circ \)
Vậy ta chọn phương án D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình vẽ, biết rằng OC là tia phân giác của \(\widehat {{\rm{BOD}}}\) và \(\widehat {{\rm{BOD}}} = 4\widehat {{\rm{AOB}}}\).
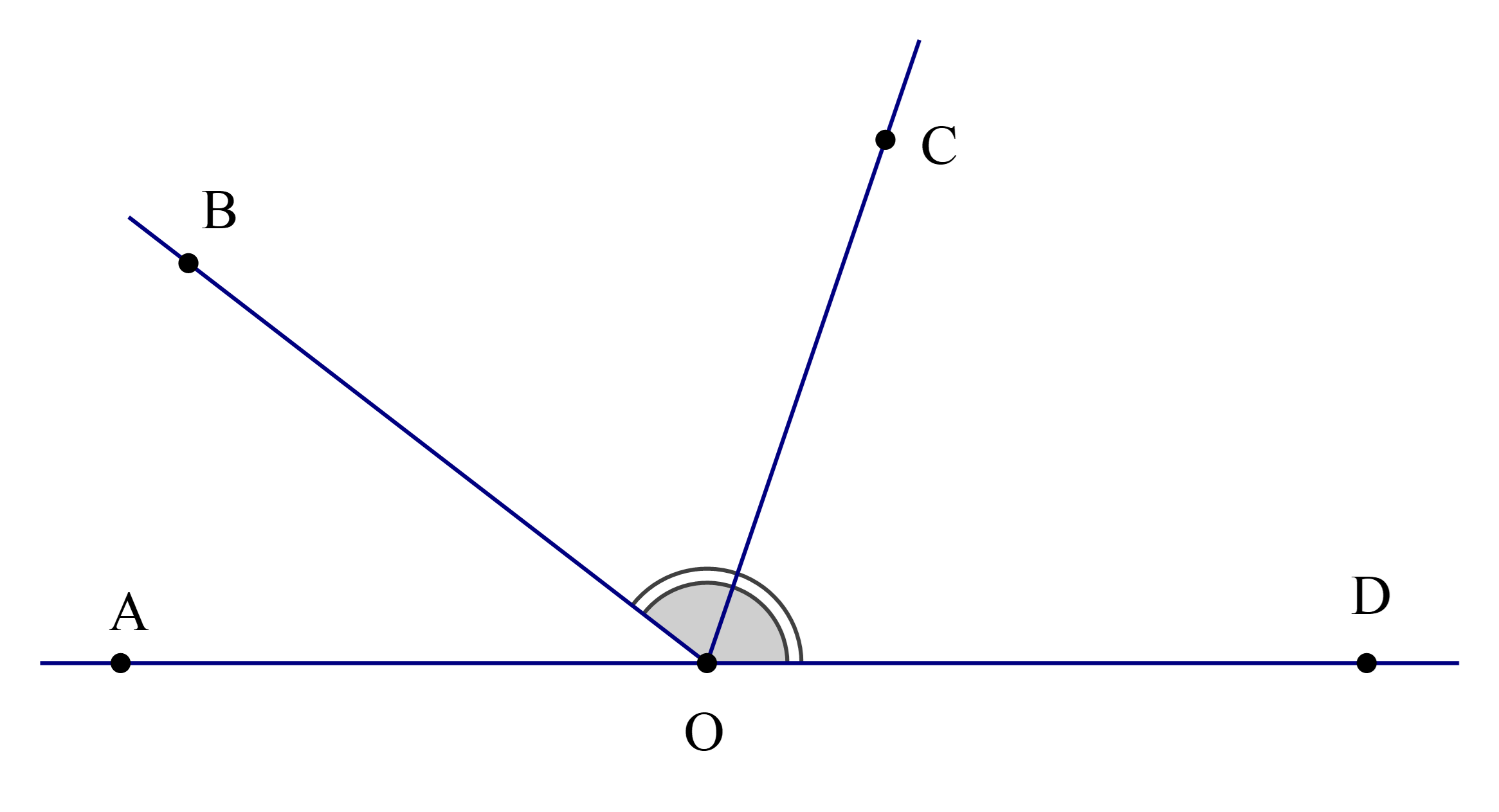
Số đo của \(\widehat {{\rm{COD}}}\) là
Cho hình vẽ.
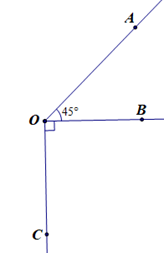
Kẻ tia OE là tia đối của tia OB và tia OD nằm giữa hai tia OC và OE sao cho \(\widehat {{\rm{COD}}} = \widehat {{\rm{DOE}}}.\) Chọn khẳng định sai:
Cho hình vẽ
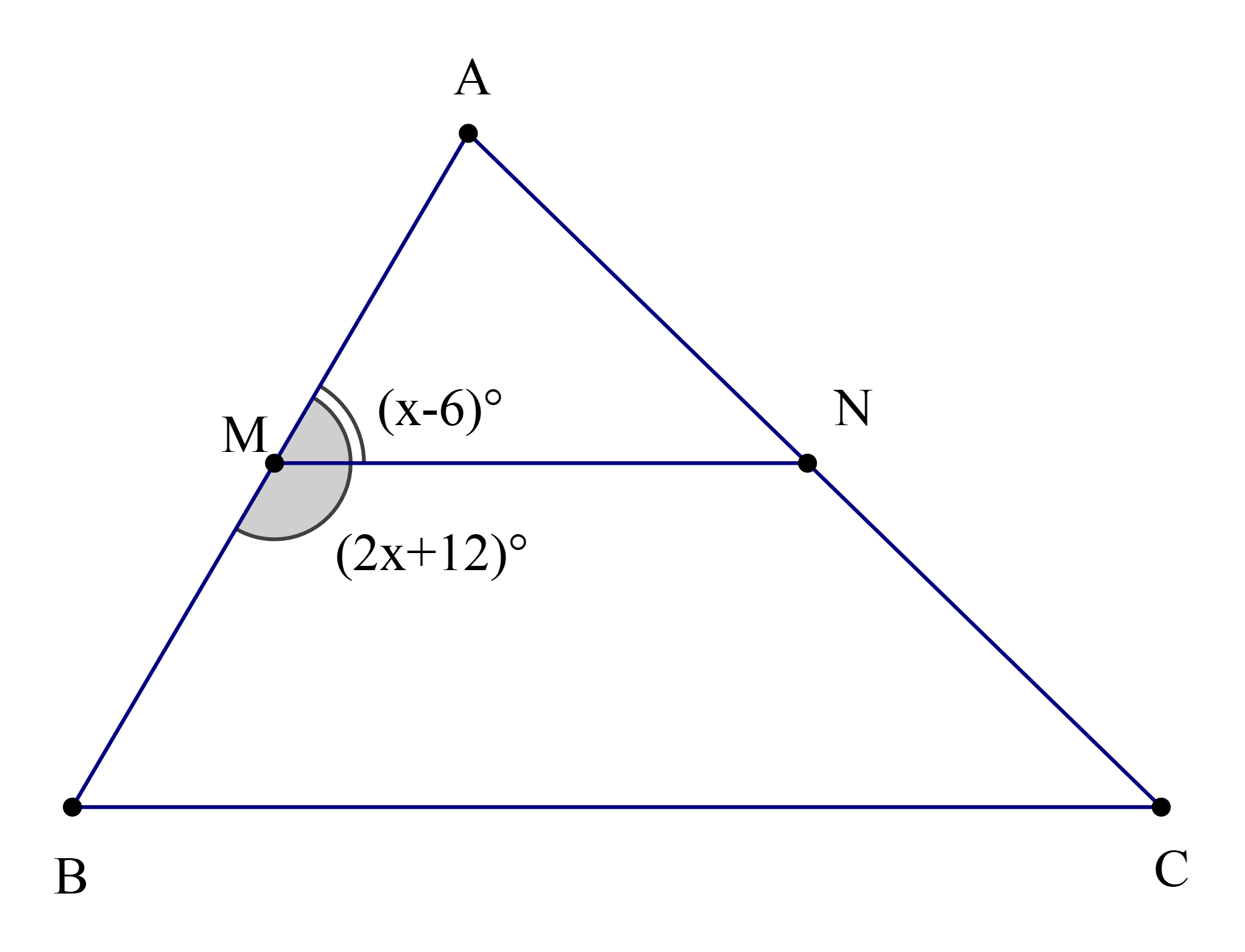
Biết rằng MN // BC. Số đó của \(\widehat {{\rm{ABC}}}\) là: