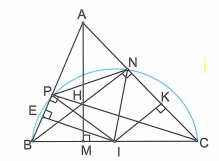
Cho tam giác nhọn ABC có trực tâm H và . Gọi M,N,P theo thứ tự là chân các đường cao kẻ từ các đỉnh A,B,C của tam giác ABC và I là trung điểm của BC.
a) Chứng minh rằng tam giác INP đều.
 Giải bởi Vietjack
Giải bởi Vietjack
a) Ta thấy và là hai tam giác vuông có chung cạnh huyền BC nên bốn điểm B,P,N,C nằm trên đường tròn tâm I, đường kính BC.
Khi đó cân tại I. (1)
Tam giác ABN vuông tại N có: .
Ta có là góc nội tiếp và là góc ở tâm cùng chắn cung .
Do đó . (2)
Từ (1) và (2) suy ra đều.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình vẽ sau:
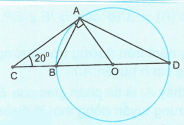
Tính số đo cung nhỏ AB và từ đó so sánh hai đoạn thẳng AC và AD.
b) Gọi E và K lần lượt là trung điểm của PB và NC. Chứng minh rằng các điểm I,M,E,K cùng thuộc một đường tròn.