Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Chứng minh rằng .
 Giải bởi Vietjack
Giải bởi Vietjack
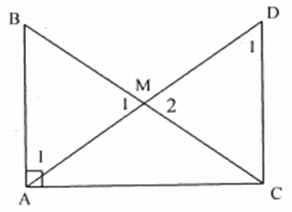
* Tìm cách giải. Để chứng minh ta cần chứng minh . Về mặt suy luận, ta cần dựng một đoạn thẳng bằng rồi chứng minh đoạn thẳng đó bằng BC.
* Trình bày lời giải.
Trên tia đối của tia MA lấy điểm D sao cho . Suy ra
và có ; ; nên .
Suy ra ; nên .
và có ; , AC chung suy ra
hay .
* Nhận xét. Bài này là một tính chất thú vị của tam giác vuông, thường được sử dụng trong những bài nối trung điểm của cạnh huyền với đỉnh góc vuông.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng ; AM=AB sao cho M và C khác phía đối với đường thẳng AB. Vẽ đoạn thẳng và AN=AC sao cho N và B khác phía đối với đường thẳng AC. Gọi I, K lần lượt là trung điểm BN và CM. Chứng minh rằng:
a,
Cho tam giác ABC. Từ B kẻ ; . Gọi H là giao điểm của BD và CE. Biết rằng .
Cho . Gọi D; E theo thứ tự là trung điểm của AB, AC. Trên tia đối của tia ED lấy điểm F sao cho EF=ED. Chứng minh:
a, ,
Cho có . Gọi M là trung điểm cạnh BC. Trên nửa mặt phẳng bờ AB không chứa điểm C kẻ tia Ax vuông góc với AB, trên tia Ax lấy điểm D sao cho AD= AB. Trên nửa mặt phẳng bờ AC không chứa điểm B kẻ Ay vuông góc với AC. Trên tia Ay lấy điểm E sao cho . Trên tia đối tia MA lấy MN= MA. Chứng minh rằng:
a,
Cho tam giác ABC có . Các tia phân giác góc B, góc C cắt nhau tại O và cắt AC; AB theo thứ tự D; E. Chứng minh rằng: OD=OE.
Cho có . Lấy M thuộc cạnh AB; lấy N thuộc tia đối của tia CA sao cho CM=BM. Gọi I là một điểm sao cho ; IM=IN. Chứng minh rằng: .
Để đo khoảng cách AB mà không đo trực tiếp, người ta đã thực hiện như sau:
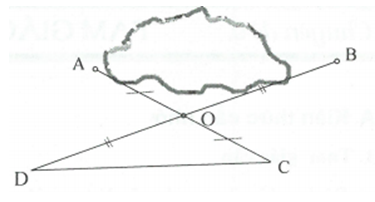
- Chọn vị trí điểm O.
- Lấy điểm C trên tia đối tia OA sao cho .
- Lấy điểm D trên tia đối tia OB sao cho .
- Đo độ dài đoạn thẳng CD, đó chính là khoảng cách AB. Hãy giải thích tại sao?
Cho tam giác ABC có , tia phân giác của cắt BC tại D. Trên AD lấy điểm O, trên tia đối của tia AC lấy điểm M sao cho . Trên tia đối của tia AB lấy điểm N sao cho . Chứng minh rằng .
Cho .
a) Viết kí hiệu về sự bằng nhau của hai tam giác đó với ba cách khác.