Cho hình vuông ABCD. Hỏi trong bốn đỉnh của hình vuông
a) Đỉnh nào cách đều hai điểm A và C?
 Giải bởi Vietjack
Giải bởi Vietjack
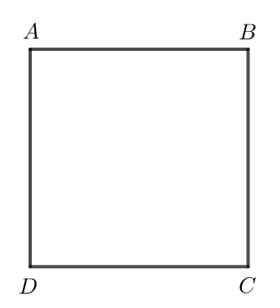
a) Do ABCD là hình vuông nên AB = BC = CD = DA.
Do CD = DA nên D cách đều hai điểm A và C.
Do AB = BC nên B cách đều hai điểm A và C.
Vậy B và D cách đều hai điểm A và C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Bạn Nam tập bơi ở một bể bơi hình chữ nhật, trong đó có ba đường bơi OA, OB, OC. Biết rằng OA vuông góc với cạnh của bể bơi (H.9,8).
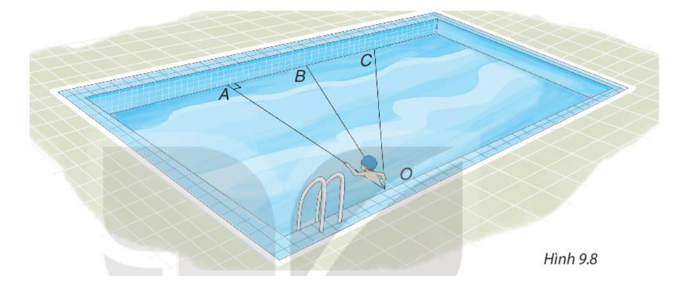
Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì bạn Nam nên chọn đường bơi nào?
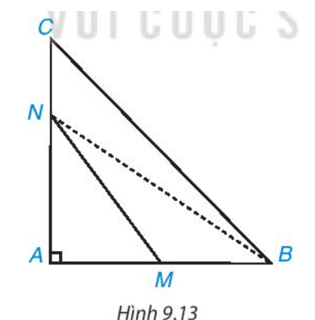
Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC
(M, N không phải là đỉnh của tam giác) (H.9.13). Chứng minh rằng MN < BC.
(Gợi ý. So sánh MN với NB, NB với BC).
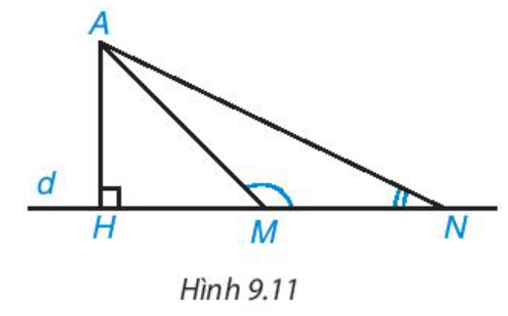
a) Quan sát Hình 9.11, ta thấy khi M thay đổi trên d, M càng xa H thì độ dài AM càng lớn, tức là nếu HM < HN thì AM < AN. Hãy chứng minh khẳng định này nhờ quan hệ giữa góc và cạnh đối diện trong tam giác AMN.
Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.12).
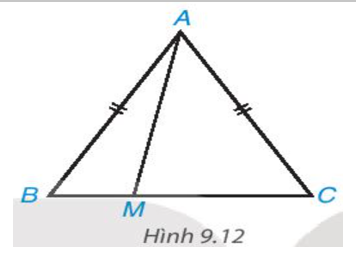
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10.
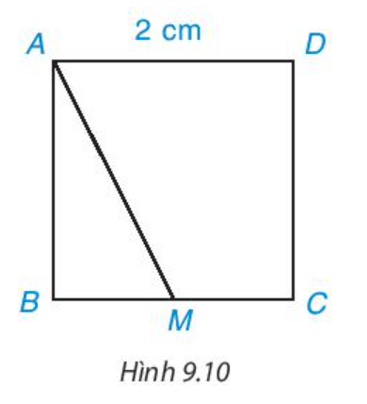
a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.
Chiều cao của tam giác ứng với một cạnh của nó có phải là khoảng cách từ đỉnh đối diện đến đường thẳng chứa cạnh đó không?
b) Xét hình vuông ABCD và một điểm M tùy ý nằm trên các cạnh của hình vuông. Hỏi với vị trí nào của M thì AM lớn nhất? Vì sao?
Cho điểm A không nằm trên đường thẳng d.
a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d.