 Giải bởi Vietjack
Giải bởi Vietjack
![]()
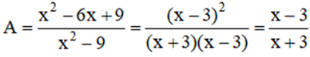
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Phân thức đối của phân thức có kết quả là:
Cho phân thức
c) Có giá trị nào của x để giá trị của phân thức A bằng 0 hay không?