Cho hình bình hành ABCD. Trên các cạnh AB, BC, CD, DA lấy các điểm I, J, K, L sao cho AI = BJ = CK = DL. Chứng minh rằng:
a) Tứ giác IJKL là hình bình hành.
b) Bốn đường thẳng AC, BD, IK, JL đồng quy
Giải bởi Vietjack
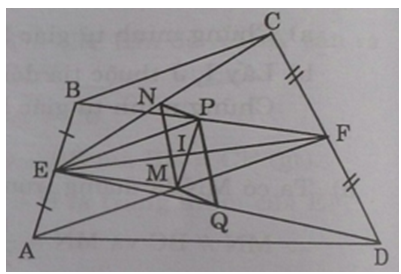
a) Ta có: BI + AI = AB
KD + CK = CD
Mà AI = CK; AB = CD
⇒ BI = KD
Xét ΔIBJ và ΔKDL có:
IB = KD
∠(IBJ) = ∠(KDL) (do ABCD là hình bình hành)
BJ = LD (gt)
⇒ ΔIBJ = ΔKDL (c.g.c)
⇒ IJ = KL
Chứng minh tương tự: ΔJCK= ΔLAI
⇒ JK = IL
Vậy tứ giác IJKL là hình bình hành (các cạnh đối bằng nhau)
b) Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD ta có O là trung điểm của AC.
Lại có tứ giác AICK là hình bình hành (AI // CK và AI = CK )
⇒ đường chéo IK đi qua trung điểm O của AC.
Tứ giác IJKL là hình bình hành (cmt) ⇒ đường chéo JL đi qua trung điểm O của đường chéo IK.
Vậy bốn đường thẳng AC, BD, IK, JL đồng quy tại O.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
