Giải bài tập Toán 10 Chủ đề 2: Xây dựng mô hình hàm số bậc nhất, bậc hai biểu diễn số liệu dạng bảng 

Hoạt động 1 trang 59 Toán 10 Tập 2: Học sinh được chia theo nhóm. Mỗi nhóm lựa chọn dữ liệu (quy mô dân số của địa phương; nhiệt độ vào các tháng ở địa phương; số giờ tự học và điểm số tương ứng; nhu cầu về một loại sản phẩm; …) và phân công thu thập dữ liệu. Sau đó mỗi nhóm điền kết quả thu thập dữ liệu vào bảng.

Sau đây là mẫu nếu lựa chọn dữ liệu là nhiệt độ vào các tháng của địa phương.

Lời giải

Mỗi nhóm lựa chọn dữ liệu và phân công nhau thu thập dữ liệu về một đề tài nào đó. Sau đây là một ví dụ khi nhóm lựa chọn đề tài về tỉ lệ sinh của Việt Nam qua các năm 2017, 2018, 2019, 2020 .

Ta thu thập được bảng dữ liệu như sau:

Hoạt động 2 trang 59 Toán 10 Tập 2: Mỗi nhóm thực hành xây dựng mô hình toán học dạng hàm số bậc nhất hoặc hàm số bậc hai để biểu diễn số liệu ở bảng thống kê theo các bước đã nêu ở mục I.2.

Lời giải

Theo đề tài ở hoạt động 1, ta xây dựng mô hình toán học dạng hàm số bậc nhất như sau:

Bước 1. Lựa chọn cách biểu diễn dữ liệu trên mặt phẳng tọa độ.

Đặt x = t – 2017 với t ∈ {2017, 2018, 2019, 2020}. Do đó ta có x ∈ {0; 1; 2; 3}.

Từ bảng ở hoạt động 1, ta có bảng thống kê như sau:

Xét các điểm A(0; 1,98), B(1; 1,98), C(2; 1,98), D(3; 2,06) trong mặt phẳng tọa độ.

Bước 2. Xem tỉ lệ sinh mỗi năm f(x) là hàm số của x. Ta phải chọn f(x) là hàm số bậc nhất sao cho f(x) dự đoán (càng chính xác càng tốt) nhiệt độ ở những năm sau năm 2020, tức là tính được giá trị của f(x) với x ≥ 4.

Căn cứ vào bốn điểm A(0; 1,98), B(1; 1,98), C(2; 1,98), D(3; 2,06) ta chọn hàm số bậc nhất y = f(x) có đồ thị “gần” nhất với bốn điểm trên.

Thông thường việc tính toán trực tiếp để xác định được công thức của hàm số bậc nhất nói trên là không dễ dàng. Người ta dùng các phần mềm toán học để trợ giúp cho quá trình tính toán. Chẳng hạn, ta sử dụng phần mềm GeoGebra để xác định hàm số bậc nhất nói trên như sau:

Vào phần mềm GeoGebra, xuất diện giao diện như hình sau:

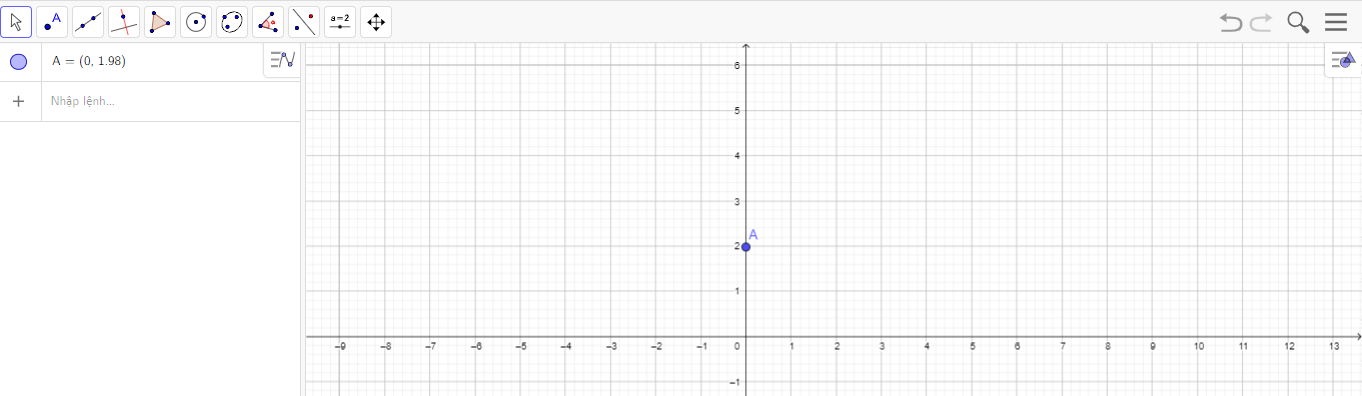
- Vẽ điểm A(0; 1,98) bằng cách dùng câu lệnh “=(0, 1.98)”, ta được như hình sau

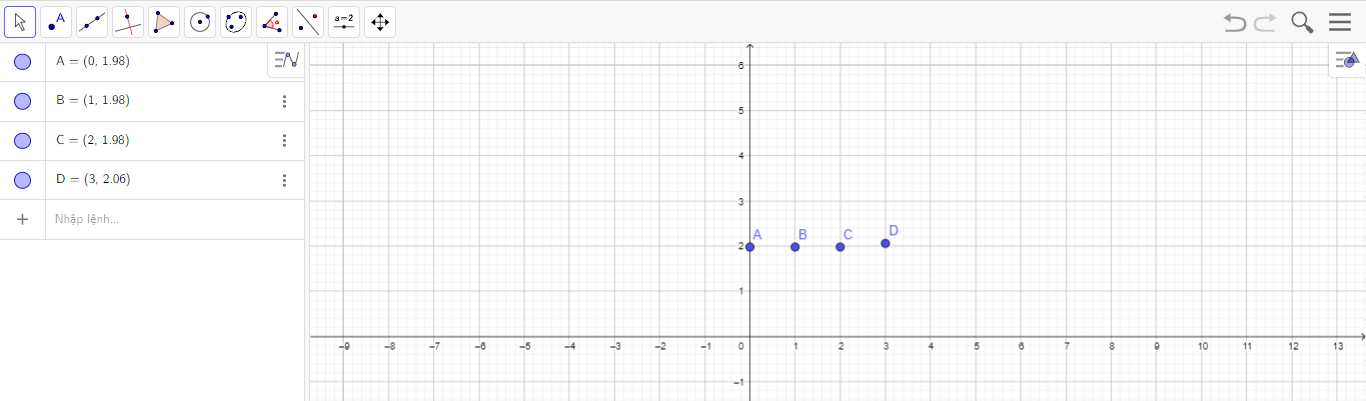
- Tương tự, vẽ các điểm B(1; 1,98), C(2; 1,98) và D(3; 2,06) trong mặt phẳng tọa độ bằng cách dùng các câu lệnh: “=(1, 1.98)”; “=(2, 1.98)”; “=(3, 2.06)”, ta được như hình sau:

- Sử dụng câu lệnh:

“=FitPoly({A,B,C,D},1)” như hình sau:

ta được hàm: f(x) = 1,04x + 19,4 với đồ thị ở hình sau:

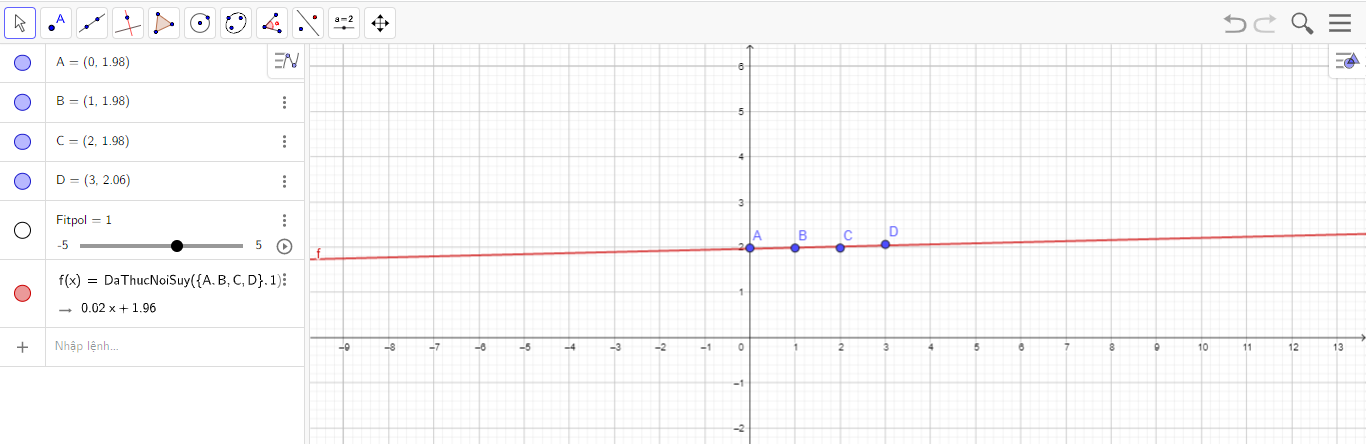
Bước 3. Dựa theo mô hình hàm số bậc nhất f(x) = 0,02x + 1,96, ta dự đoán được tỉ lệ sinh của các năm 2021, 2022, 2023... lần lượt là:

f(4) = 0,02 . 4 + 1,96 = 2,04;

f(5) = 0,02 . 5 + 1,96 = 2,06;

f(6) = 0,02 . 6 + 1,96 = 2,08.

Bước 4. Dự đoán trên là hợp lí, vì thế ta không cần điều chỉnh mô hình toán học đã chọn.