Giải bài tập Toán 10 Bài tập cuối chương 1 trang 19

Video giải bài tập Toán 10 Bài tập cuối chương 1 trang 19 

Bài 1 trang 19 Toán lớp 10 Tập 1: Phát biểu nào sau đây là một mệnh đề toán học?

a) Tích của ba số tự nhiên liên tiếp luôn chia hết cho 3.

b) Nếu $\widehat{AMB}=90°$ thì M nằm trên đường tròn đường kính AB.

c) Ngày 2 tháng 9 là ngày Quốc Khánh của nước Cộng hòa Xã hội chủ nghĩa Việt Nam.

Lời giải:

Trong các phát biểu đã cho, có phát biểu a, b, d là các mệnh đề toán học vì cả ba phát biểu đều là khẳng định một sự kiện trong toán học.

Phát biểu ở câu c không phải mệnh đề toán học.

Bài 2 trang 19 Toán lớp 10 Tập 1: Lập mệnh đề phủ định của mỗi mệnh đề sau và nhận xét tính đúng sai của mệnh đề phủ định đó.

A: “Đồ thị hàm số y = x là một đường thẳng”.

B: “Đồ thị hàm số y = x² đi qua điểm A(3; 9)”.

Lời giải:

+ A: “Đồ thị hàm số y = x là một đường thẳng”

 Mệnh đề phủ định của mệnh đề A là mệnh đề $\overline{A}$: “Đồ thị hàm số y = x không phải là một đường thẳng”.

Đồ thị của hàm số y = x là đường thẳng đi qua gốc tọa độ. Suy ra mệnh đề A là mệnh đề đúng. Do đó mệnh đề phủ định $\overline{A}$ là mệnh đề sai.

+ B: “Đồ thị hàm số y = x² đi qua điểm A(3; 9)”

Mệnh đề phủ định của mệnh đề B là mệnh đề $\overline{B}$: “Đồ thị của hàm số y = x² không đi qua điểm A(3; 9)”.

Thay x = 3 và y = 9 vào y = x², ta được:

9 = 3² hay 9 = 9 (luôn đúng)

Do đó điểm A thuộc vào đồ thị hàm số y = x² hay đồ thị của hàm số y = x² đi qua điểm A(3; 9).

Suy ra mệnh đề B là mệnh đề sai và mệnh đề $\overline{B}$ là mệnh đề đúng.

Bài 3 trang 19 Toán lớp 10 Tập 1: Cho tứ giác ABCD. Lập mệnh đề P ⇒ Q và xét tính đúng sai của mệnh đề đó với:

a) P: “Tứ giác ABCD là hình chữ nhật”, Q: “Tứ giác ABCD là hình bình hành”;

b) P: “Tứ giác ABCD là hình thoi”, Q: “Tứ giác ABCD là hình vuông”. 

Lời giải:

a) Mệnh đề P ⇒ Q: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD là hình bình hành”.

Ta có tứ giác ABCD là hình chữ nhật thì AB // CD và AB = CD

 Suy ra tứ giác ABCD là hình bình hành (theo một số yếu tố cơ bản của hình bình hành).

Do đó mệnh đề P ⇒ Q đúng.

b) Mệnh đề P ⇒ Q: “Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD là hình vuông”.

Ta có tứ giác ABCD là hình thoi nên tứ giác ABCD có bốn cạnh bằng nhau nhưng bốn góc của tứ giác ABCD không bằng nhau. Suy ra tứ giác ABCD không phải là hình vuông.

Do đó mệnh đề P ⇒ Q là mệnh đề sai.

Bài 4 trang 19 Toán lớp 10 Tập 1: Lập mệnh đề phủ định của mỗi mệnh đề sau:

A: “ $\forall x\in ℝ$, |x| ≥ x”;

B: “$\forall x\in ℝ$ ,$x+\frac{1}{x}\ge 2$ ”;

C: “ $\exists x\in \mathbb{Z},$2x² + 3x – 2 = 0”;

D: “ $\exists x\in \mathbb{Z},$x² < x”.

Lời giải:

+ Mệnh đề phủ định của mệnh đề A là mệnh đề $\overline{A}$: “$\exists x\in ℝ,$|x| < x”.

+ Mệnh đề phủ định của mệnh đề B là mệnh đề $\overline{B}$: “$\exists x\in ℝ,x+\frac{1}{x}<2$”.

+ Mệnh đề phủ định của mệnh đề C là mệnh đề $\overline{C}$: “$\forall x\in \mathbb{Z}$, 2x² + 3x – 2 ≠ 0”.

+ Mệnh đề phủ định của mệnh đề D là mệnh đề $\overline{D}$: “$\forall x\in \mathbb{Z}$, x² ≥ x”.

Bài 5 trang 19 Toán lớp 10 Tập 1: Dùng kí hiệu để viết mỗi tập hợp sau và biểu diễn mỗi tập hợp đó trên trục số.

a) A = {x$\in ℝ$ | – 2 < x < – 1};

b) B = {x$\in ℝ$ | – 3 ≤ x ≤ 0};

c) C = {x$\in ℝ$ | x ≤ 1};

d) D = {x $\in ℝ$| x > – 2}.

Lời giải:

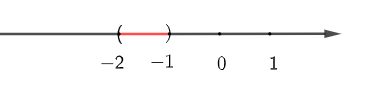
a) Biểu diễn tập hợp A bằng kí hiệu ta được: A = {x $\in ℝ$| – 2 < x < – 1} =  (–2 ; – 1)

Biểu diễn tập hợp A trên trục số là phần màu đỏ:

b) Biểu diễn tập hợp B bằng kí hiệu ta được: B = {x $\in ℝ$| – 3 ≤ x ≤ 0} = [– 3; 0]

Biểu diễn tập hợp B trên trục số là phần màu đỏ:

c) Biểu diễn tập hợp C bằng kí hiệu ta được: C = {x $\in ℝ$| x ≤ 1} = (– ∞; 1]

Biểu diễn tập hợp C trên trục số là phần màu đỏ:

d) Biểu diễn tập hợp D bằng kí hiệu ta được: D = {x $\in ℝ$| x > – 2} = (– 2; +∞)

Biểu diễn tập hợp D trên trục số là phần màu đỏ:

Bài 6 trang 19 Toán lớp 10 Tập 1: Giải Bóng đá vô địch thế giới World Cup 2018 được tổ chức ở Liên bang Nga gồm 32 đội. Sau vòng thi đấu bảng, Ban tổ chức chọn ra 16 đội chia làm 8 cặp đấu loại trực tiếp. Sau vòng đấu loại trực tiếp đó, Ban tổ chức tiếp tục chọn ra 8 đội chia làm 4 cặp đấu loại trực tiếp ở vòng tứ kết. Gọi A là tập hợp 32 đội tham gia World Cup năm 2018, B là tập hợp 16 đội sau vòng thi đấu bảng, C là tập hợp 8 đội thi đấu vòng tứ kết.

a) Sắp xếp các tập hợp A, B, C theo quan hệ “⊂”. 

b) So sánh hai tập hợp A ∩ C và B ∩ C. 

c) Tập hợp A \ B gồm những đội bóng bị loại sau vòng đấu nào? 

Lời giải:

a) Ta thấy 8 đội ở vòng đấu tứ kết được chọn từ 16 đội ở vòng đấu loại trực tiếp và 16 đội ở vòng loại trực tiếp được chọn từ 32 đội tham gia World Cup năm 2018.

Do đó các phần tử thuộc tập hợp C đều thuộc tập hợp B và các phần tử của tập hợp B đều thuộc tập hợp A. Vì vậy các phần tử của tập hợp C cũng thuộc tập hợp A.

Suy ra C là tập con của B và B là tập con của A hay C ⊂ B ⊂ A.

Vậy C ⊂ B ⊂ A.

b) Vì C ⊂ A nên A ∩ C = C

Vì C ⊂ B nên B ∩ C = C

Suy ra A ∩ C = B ∩ C = C.

Vậy A ∩ C = B ∩ C.

c) Tập hợp A \ B là tập hợp các đội bóng thuộc A nhưng không thuộc B.

Mà A là tập hợp 32 đội tham gia World Cup năm 2018, B là tập hợp 16 đội ở vòng đấu loại trực tiếp.

Điều này có nghĩa là tập hợp A \ B gồm những đội bóng bị loại ở vòng thi đấu bảng.

Bài 7 trang 19 Toán lớp 10 Tập 1: Cho hai tập hợp: A = [0; 3], B = (2; + ∞).

Xác định A ∩ B, A ∪ B, A \ B, B \ A, $ℝ$\ B. 

Lời giải:

+ Ta có: A =  [0; 3] = {x $\in ℝ$| 0 ≤ x ≤ 3} và B = (2; + ∞) = {x $\in ℝ$| x > 2}.

Suy ra A ∩ B = {x $\in ℝ$| 2 < x ≤ 3} = (2; 3].

Vậy A ∩ B = [0; 3] ∩ (2; + ∞) = (2; 3].

+ Ta có: A = [0; 3] = {x $\in ℝ$| 0 ≤ x ≤ 3} và B = (2; + ∞) = {x $\in ℝ$| x > 2}.

Suy ra A ∪ B =  {x $\in ℝ$| x ≥ 0} = [0; + ∞).

Vậy A ∪ B = [0; 3] ∪ (2; + ∞) = [0; + ∞).

+ Ta có: A = [0; 3] = {x $\in ℝ$| 0 ≤ x ≤ 3} và B = (2; + ∞) = {x $\in ℝ$| x > 2}.

Suy ra A \ B = {x $\in ℝ$| 0 ≤ x ≤ 2} = [0; 2].

Vậy A \ B = [0; 3] \ (2; + ∞) = [0; 2].

+ Ta có: A = [0; 3] = {x $\in ℝ$| 0 ≤ x ≤ 3} và B = (2; + ∞) = {x $\in ℝ$| x > 2}.

Suy ra B \ A = {x $\in ℝ$| x > 3} = (3; + ∞).

Vậy B \ A =  (2; + ∞) \ [0; 3] = (3; + ∞).

+ Tập hợp $ℝ$\ B là tập hợp các số thực không thuộc tập hợp B

Vậy $ℝ$\ B = $ℝ$ \ (2; + ∞) = (– ∞; 2].

Bài 8 trang 19 Toán lớp 10 Tập 1: Gọi E là tập nghiệm của phương trình x² – 2x – 3 = 0, G là tập nghiệm của phương trình (x + 1)(2x – 3) = 0.

Tìm P = E ∩ G.

Lời giải:

+ Xét phương trình x² – 2x – 3 = 0

⇔ x² + x – 3x – 3 = 0

⇔ x(x + 1) – 3(x +1) = 0

⇔ (x + 1)(x – 3) = 0

$\iff \left[\begin{array}{l}x+1=0\\ x-3=0\end{array}\right.\iff \left[\begin{array}{l}x=-1\\ x=3\end{array}\right.$.

Suy ra phương trình trên có hai nghiệm là 3 và – 1.

Do đó E = {– 1; 3}.

+ Ta có: (x + 1)(2x – 3) = 0

$\iff \left[\begin{array}{l}x+1=0\\ 2x-3=0\end{array}\right.\iff \left[\begin{array}{l}x=-1\\ x=\frac{3}{2}\end{array}\right.$

Do đó G = $\left\{-1;\frac{3}{2}\right\}$

Ta có P = E ∩ G hay P là giao của hai tập hợp E và G, gồm các phần tử vừa thuộc E vừa thuộc G.

Vậy P = E ∩ G = {– 1; 3}$\cap \left\{-1;\frac{3}{2}\right\}$ = {– 1}.