Cho hình vẽ sau:
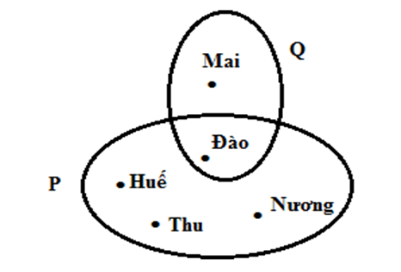
Viết tập hợp P và Q.
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có P={Huế; Thu; Nương; Đào}
Q={Đào; Mai}
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho A là tập hợp các số chẵn lớn hơn 15. Số nào trong các số sau là một phần tử của A?
A là tập hợp tên các hình trong Hình 3:

Khẳng định nào sau đây đúng?
Cho tập hợp E = {0; 2; 4; 6; 8}. Hãy chỉ ra tính chất đặc trưng cho các phần tử của tập hợp E.
Hệ Mặt Trời gồm có Mặt Trời ở trung tâm và 8 thiên thể quanh quanh Mặt Trời gọi là các hành tinh. Đó là sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương.
Cho S là tập hợp các hành tinh của Hệ Mặt Trời. Khẳng định nào sau đây đúng?
Số phần tử của tập hợp P gồm các chữ cái trong cụm từ “ WORLD CUP” là
Cho B là tập hợp các số tự nhiên nhỏ hơn 10. Trong các khẳng định sau, có bao nhiêu khẳng định sai?
1.
2.
3.
4.
5.
1. Tập hợp và phần tử của tập hợp
Tập hợp là một khái niệm cơ bản của toán học (không định nghĩa).
Tập hợp được kí hiệu là các chữ cái in hoa: A, B, C, D, …
Ví dụ 1.
a) Tập hợp các học sinh trong tổ 4 của 6A là: Thắm, Trọng, Xuân, Cương, Bảo, Dũng, Khôi, Huế, Linh.
b) Tập hợp các loại bút bên trong túi bút của bạn Ngọc là: Bút bi, bút chì, bút đánh dấu, bút xóa, bút màu.
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định. Các đối tượng ấy được gọi là những phần tử của tập hợp.

x là một phần tử của tập hợp A. Kí hiệu x ∈ A (đọc là x thuộc A).
y không là một phần tử của tập hợp A. Kí hiệu y ∉ A (đọc là y không thuộc A).
Chú ý: Khi x thuộc A, ta còn nói “x nằm trong A”, hay “A chứa x”.
Ví dụ 2. Cho tập hợp M như hình vẽ. Những phần tử nào thuộc tập hợp M, những phần tử nào không thuộc tập hợp M?
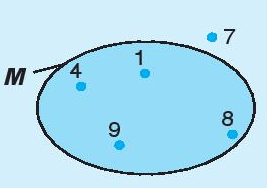
Tập hợp M gồm các phần tử 1; 4; 8; 9.
Ta có 1 là một phần tử của tập hợp M. Kí hiệu 1 ∈ M .
4 là một phần tử thuộc tập hợp M. Kí hiệu 4 ∈ M .
8 là một phần tử thuộc tập hợp M. Kí hiệu 8 ∈ M .
9 là một phần tử thuộc tập hợp M. Kí hiệu 9 ∈ M .
7 không là phần tử thuộc tập hợp M. Kí hiệu 7 ∉ M
2. Mô tả một tập hợp
2.1. Liệt kê các phần tử của tập hợp
Viết tất cả các phần tử của tập hợp trong dấu {} theo thứ tự tùy ý nhưng mỗi phần tử chỉ được viết một lần.
Ví dụ 3. Cho hình vẽ:
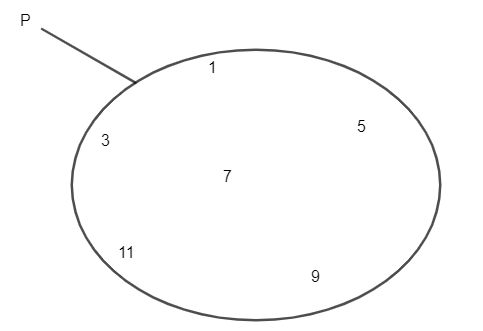
Với tập hợp P gồm các số 1; 3; 5; 7; 9; 11 như hình vẽ.
Theo cách liệt kê, ta viết: P = {1; 3; 5; 7; 9; 11}.
2.1. Nêu dấu hiệu đặc trưng cho các phần tử của tập hợp
Gọi x là phần tử của tập hợp, chỉ ra tính chất đặc trưng của phần tử và viết tập hợp đã cho.
Ví dụ 4. Với tập hợp P = {1; 3; 5; 7; 9; 11}.
Ta thấy các phần tử của tập hợp P là các số tự nhiên lẻ và nhỏ hơn 12.
Khi đó, theo cách chỉ ra đặc trưng tập hợp P được viết là:
P = {x | x là số tự nhiên lẻ và nhỏ hơn 12}.
B. Bài tập
Bài 1. Cho tập hợp E như hình vẽ:
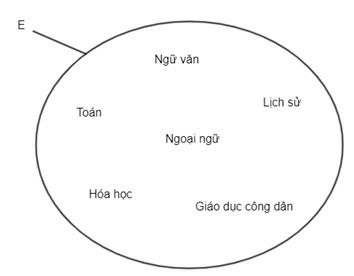
a) Hãy viết tập hợp E bằng cách liệt kê các phần tử của tập hợp.
b) Điền dấu ( ∈, ∉ ) thích hợp vào ô trống.
Ngữ văn  E; Toán
E; Toán  E; Vật lý
E; Vật lý  E;
E;
Địa lý  E; Ngoại ngữ
E; Ngoại ngữ  E; Lịch sử
E; Lịch sử  E.
E.
Lời giải
a) Bằng cách liệt kê các phần tử của tập hợp, ta viết:
E = {Toán; Ngữ văn; Lịch sử; Ngoại ngữ; Giáo dục công dân; Hóa học}.
b)
Ngữ văn 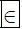 E; Toán
E; Toán 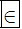 E; Vật lý
E; Vật lý 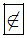 E;
E;
Địa lý 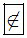 E; Ngoại ngữ
E; Ngoại ngữ 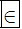 E; Lịch sử
E; Lịch sử 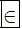 E.
E.
Bài 2. Viết các tập hợp sau bằng cách chỉ ra tính chất đặc trưng của chúng:
a) A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} ;
b) B = {1; 2; 3; 4; 5; 6; 7; 8; 9} .
Lời giải
a) Ta thấy các phần tử của tập hợp A là các số tự nhiên nhỏ hơn 10.
Bằng cách chỉ ta tính chất đặc trưng, ta viết: A = {x ∈ N | x < 10}.
b) Ta thấy các phần tử của tập hợp A là các số tự nhiên khác 0 nhỏ hơn 10.
Bằng cách chỉ ra tính chất đặc trưng, ta viết: A = {x ∈ N* | x < 10}.