Thay a và b bằng một số tự nhiên phù hợp trong trường hợp sau:

17, b, a là ba số lẻ liên tiếp tăng dần.

1. Hệ thập phân

+ Cách ghi số tự nhiên trong hệ thập phân

- Trong hệ thập phân, mỗi số tự nhiên được viết dưới dạng một dãy những chữ số lấy trong 10 chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8 và 9; vị trí của các chữ số trong dãy gọi là hàng.

- Cứ 10 đơn vị ở một hàng thì bằng 1 đơn vị ở hàng liền trước nó. Chẳng hạn, 10 chục thì bằng 1 trăm; 10 trăm thì bằng 1 nghìn; …

Chú ý: Khi viết các số tự nhiên ta quy ước:

1. Với các số tự nhiên khác 0, chữ số đầu tiên (từ trái sang phải) khác 0.

2. Để dễ đọc với các số có bốn chữ số ta viết tách riêng từng lớp. Mỗi lớp là một nhóm ba chữ số kể từ phải sang trái.

Ví dụ 1. Hãy viết tất cả các số tự nhiên có ba chữ số khác nhau chỉ dùng 3 chữ số 0; 3; 5. Đọc mỗi số đã viết được.

Lời giải

Các số tự nhiên có ba chữ số khác nhau từ ba số 0; 3; 5 là:

305; 350; 503; 530.

Cách đọc:

305: ba trăm linh năm;

350: ba trăm năm mươi;

503: năm trăm linh ba;

530: năm trăm ba mươi.

+ Mỗi số tự nhiên viết trong hệ thập phân đều biểu diễn được thành tổng giá trị các chữ số của nó. Chẳng hạn như số có ba chữ số 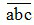(a, b, c ∈ N) được viết dưới dạng tổng giá trị các chữ số của nó như sau: 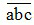= a x 100 + b x 10 + c

Ví dụ 2. 

a) Viết sô 32009 thành tổng các chữ số của chúng.

c) Cho số 1256934, chữ số 5 trong số đã cho nằm ở hàng nào và có giá trị bao nhiêu?

Lời giải

a) 32009 = 3 x 10000 + 2 x 1000 + 0 x 100 + 0 x 10 + 9.

b) Chữ số 5 trong số đã cho nằm ở hàng chục nghìn và có giá trị .

2. Số La Mã

Để viết các số La Mã không quá 30, ta dùng các kí tự I, V và X (gọi là những số La Mã).

Ba chữ số đó cộng với hai cụm chữ số là IV và IX là năm thành phần dùng để ghi số La Mã. 

Giá trị của mỗi thành phần được ghi lại trong bảng sau và không thay đổi dù đứng ở bất kì vị trí nào:

+ Dưới đây là các số La Mã biểu diễn các số từ 1 đến 10:

+ Để biểu diễn các số từ 11 đến 20, ta thêm X vào bên trái mỗi số từ I đến X:

+ Để biểu diễn các số từ 21 đến 30, ta thêm XX vào bên trái mỗi số từ I đến X:

Ví dụ 3:

a) Viết các số 17; 23 và 8 bằng số La Mã.

b) Đọc các số La Mã XXIX, XIV, VII.

Lời giải

a) Số La Mã biểu diễn cho số 17 là: XVII;

Số La Mã biểu diễn cho số 23 là: XXIII;

Số La Mã biểu diễn cho số 8 là: VIII.

b) Đọc:

XXIX: Hai mươi chín;

XIV: Mười bốn;

VII: Bảy.

B. Bài tập

Bài 1. Một chữ số được viết bởi ba chữ số 5 nằm giữa hai chữ số 2. Đó là số nào? Và viết số đó thành tổng giá trị các chữ số của nó.

Lời giải

Số cần tìm là: 25 552.

Ta có: 25552 = 2 x 10000 + 5 x 1000 + 5 x 100 + 5 x 10 + 2.

Bài 2. Chữ số 3 đứng ở hàng nào trong một số tự nhiên nếu nó có giá trị:

a) 30 000 000;

b) 300.

Lời giải

a) Nếu chữ số 3 có giá trị 30 000 000 thì nó đang đứng ở hàng chục triệu.

b) Nếu chữ số 3 có giá trị 300 thì nó đnag đứng ở hàng trăm.

Bài 3. Đọc các số La Mã sau: XVIII, XX, XXI.

Lời giải

XVIII: Mười tám;

XX: Hai mươi;

XXI: Hai mươi mốt.