Một hình vuông có diện tích là 1936m2. Tính cạnh của hình vuông đó.
 Giải bởi Vietjack
Giải bởi Vietjack
Trả lời:
Phân tích số 1936 ra thừa số nguyên tố ta được
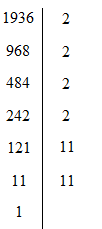
Hay 1936 = 24.112 = (22.11).(22.11) = 44.44
Vậy cạnh hình vuông bằng 44m.
Đáp án cần chọn là: A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Nếu cho 7 hình vuông đơn vị ghép thành hình chữ nhật thì có mấy cách xếp (Không kể việc xoay chiều dài và chiều rộng)?
Tổng của 3 số nguyên tố là 578. Tìm ra số nguyên tố nhỏ nhất trong 3 số nguyên tố đó.
Số 360 khi phân tích được thành thừa số nguyên tố, hỏi tích đó có bao nhiêu thừa số là số nguyên tố?
Khi phân tích các số 2150; 1490; 2340 ra thừa số nguyên tố thì số nào có chứa tất cả các thừa số nguyên tố 2; 3 và 5?
Cho A = 90.17 + 34.40 + 12.51 và B = 5.7.9 + 2.5.6
Chọn câu đúng.
Tích của hai số tự nhiên bằng 105. Có bao nhiêu cặp số thỏa mãn?
Cho phép tính \[\overline {ab} .c = 424\]. Khi đó c bằng bao nhiêu?
1. Số nguyên tố và hợp số
- Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
- Hợp số là số tự nhiên lơn hơn 1, có nhiều hơn hai ước.
Ví dụ 1. Trong các số đã cho dưới đây, số nào là số nguyên tố, số nào là hợp số? Vì sao?
190; 11; 132; 23; 43; 17; 21.
Lời giải
Ta thấy 190 có các ước là 1, 2, 5, 190 nhiều hơn hai ước nên 190 là hợp số;
11 chỉ có ước là 1 và 11 nên 11 là số nguyên tố;
132 có các ước là 1; 2; 132 nhiều hơn hai ước nên 132 là hợp số;
23 chỉ có ước là 1 và 23 nên 23 là số nguyên tố;
43 chỉ có ước là 1 và 43 nên 43 là số nguyên tố;
17 chỉ có ước là 1 và 17 nên 17 là số nguyên tố;
21 có các ước là 1; 3; 7; 21 nhiều hơn hai ước nên 21 là hợp số.
2. Phân tích một số ra thừa số nguyên tố
Mọi số đều có thể phân tích ra tích của các thừa số nguyên tố
Cách phân tích một số ra thừa số nguyên tố:
+) Phương pháp phân tích bằng sơ đồ cây
Ví dụ 2. Phân tích 36 ra tích các thừa số nguyên tố bằng sơ đồ cây:
Lời giải

Vậy 36 = 22.32.
+) Phương pháp phân tích bằng sơ đồ cột
Ví dụ 3. Phân tích 36 ra tích các thừa số nguyên tố bằng sơ đồ cột:
|
36 18 9 3 1 |
2 2 3 3 |
Vậy 36 = 22.32.