Tìm tổng các giá trị nguyên của x biết \[ - 12 < x \le - 1.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Trả lời:
Vì \[ - 12 < x \le - 1.\] nên \[x \in \{ - 11; - 10; - 9;...; - 1\} \]
Tổng cần tìm là \[( - 11) + ( - 10) + ( - 9) + ( - 8) + ... + ( - 1)\]
\[\begin{array}{l} = - (11 + 10 + 9 + ... + 1)\\ = - [(11 + 1).11:2] = - 66.\end{array}\]
Đáp án cần chọn là: A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một chiếc tàu ngầm đang ở độ cao -30m so với mực nước biển. Sau đó tàu ngầm nổi lên 25m. Độ cao mới của chiếc tàu so với mực nước biển là:
Giá trị của biểu thức \[B = 8912 + x\;\] biết \[x = - 6732\;\] là
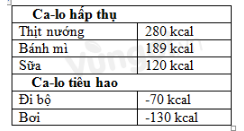
Mỗi người khi ăn thì sẽ hấp thụ ca-lo và khi hoạt động thì sẽ tiêu hao ca-lo. Bạn Bình dùng phép cộng số nguyên để tính số ca-lo hằng ngày của mình bằng cách xem số ca-lo hấp thụ là số nguyên dương và số ca-lo tiêu hao là số nguyên âm. Em hãy giúp bạn Bình kiểm tra tổng số ca-lo còn lại sau khi ăn sáng và thực hiện các hoạt động (theo số liệu trong bảng dưới đây).
Tổng \[S = 1 + ( - 3) + 5 + ( - 7) + ... + 2001 + ( - 2003)\] bằng
Một chiếc chiếc diều cao 30m ( so với mặt đất), sau một lúc độ cao của chiếc diều tăng lên 7m rồi sau đó giảm 4m. Hỏi chiếc diều ở độ cao bao nhiêu mét so với mặt đất sau 2 lần thay đổi?
Trong một ngày, nhiệt độ ở New-York lúc 6 giờ là \[ - {3^o}C\] , đến 10 giờ tăng thêm \[{7^o}C\] và lúc 13 giờ tăng thêm \[{3^o}C\] . Nhiệt độ ở New-York lúc 13 giờ là bao nhiêu?
Bác Hà là khách quen của cửa hàng tạp hóa nhà bác Diệp nên có thể mua hàng trước, trả tiền sau. Hôm qua bác Diệp đã cho bác Hà nợ 80 nghìn đồng, hôm nay bác Hà lại muốn nợ 40 nghìn đồng nữa. Em hãy dùng số nguyên để giúp bác Diệp ghi vào sổ số tiền bác Hà còn nợ bác Diệp (đơn vị: nghìn đồng).
Để di chuyền giữa các tầng của toà nhà cao tầng, người ta thường sử dụng thang máy. Tầng có mặt sàn là mặt đất thường được gọi là tầng G, các tầng ở dưới mặt đất lần lượt từ trên xuống được gọi là B1, B2,...Người ta biểu thị vị trí tầng G là 0, tầng hầm B1 là - 1, tầng hầm B2 là – 2, ...

Từ tầng G bác Sơn đi thang máy xuống tầng hầm B1. Sau đó bác đi xuống tiếp 2 tầng nữa. Tìm số nguyên biểu thị vị trí tầng mà bác Sơn đến khi kết thúc hành trình.
Một cửa hàng kinh doanh có lợi nhuận như sau: tháng đầu tiên là – 10 000 000 đồng; tháng thứ 2 là 30 000 000 đồng. Tính lợi nhuận của cửa hàng sau hai tháng đó.
Bỏ dấu ngoặc trong trường hợp đơn giản
Các số âm (hay dương) trong một dãy tính thường được viết trong dấu ngoặc. Nhờ quy tắc cộng hay trừ số nguyên, ta có thể viết dãy tính dưới dạng không có dấu ngoặc.
Vì phép trừ chuyển được về phép cộng nên các dãy tính như trên cũng được gọi là một tổng.
Ví dụ 1. Tính:
a) (-2) - (-8);
b) 3 + (-9) + (-4) – (-11).
Lời giải
a) (-2) - (-8) = -2 + 8 = 8 – 2 = 6;
b) 3 + (-9) + (-4) – (-11) = 3 – 9 – 4 + 11 = - 6 – 4 + 11 = - 10 + 11 = 1.
Quy tắc dấu ngoặc:
Khi bỏ dấu ngoặc có dấu “+” đằng trước, ta giữ nguyên dấu của các số hạng trong ngoặc;
Khi bỏ dấu ngoặc có dấu “-” đằng trước, ta phải đổi dấu tất cả các số hạng trong dấu ngoặc: dấu “+” đổi thành “-” và dấu “-” đổi thành dấu “+”.
Ví dụ 2. Bỏ dấu ngoặc và tính các tổng sau:
a) 232 – (581 + 132 – 331);
b) (56 – 27) – (11 + 28 – 16);
c) [24 + (-37)] – [-37 – (-24)];
d) -321 + (-29) – 142 – (-72).
Lời giải
a) 232 – (581 + 132 – 331)
= 232 – 581 - 132 + 331
= (232 – 132) + (-581 + 331)
= 100 + (-250)
= - (250 – 100)
= - 150.
b) (56 – 27) – (11 + 28 – 16)
= 56 – 27 – 11 – 28 + 16
= 29 – 11 – 28 + 16
= 18 – 28 + 16
= -10 + 16
= 6
c) [24 + (-37)] – [-37 – (-24)]
= 24 + (-37) + 37 – 24
= (24 – 24) + [(-37) + 37]
= 0 + 0
= 0
d) -321 + (-29) – 142 – (-72)
= - 321 + (-29) -142 + 72
= - 250 – 142 + 72
= -392 + 72
= -320
B. Bài tập
Bài 1. Tính giá trị của biểu thức:
a) (27 + 86) – (29 – 5 + 84);
b) 39 – (298 – 89) + 299.
Lời giải
a) (27 + 86) – (29 – 5 + 84)
= 27 + 86 – 29 + 5 – 84
= 113 – 29 + 5 – 84
= 84 + 5 – 84
= 89 – 84
= 5
b) 39 – (298 – 89) + 299
= 39 – 298 + 89 + 299
= - 259 + 89 + 299
= -170 + 299
= 129
Bài 2. Tính giá trị của các biểu thức sau:
a) (23 + x) – (56 – x) với x = 7;
b) 25 – x – (29 + y – 8) với x = 13, y = 11.
Lời giải
a) (23 + x) – (56 – x)
= 23 + x – 56 + x
= (23 – 56) + (x + x)
= (-33) + 2x
Thay x = 7 vào biểu thức trên, ta được:
(-33) + 2.7 = (-33) + 14 = - (33 – 14) = - 19.
b) 25 – x – (29 + y – 8)
= 25 – x – 29 – y + 8
= (25 – 29 + 8) – x – y
= 4 – x – y
Thay x = 13, y = 11 vào biểu thức trên ta được:
4 – 13 – 11 = - 9 – 11 = - (9 + 11) = -20.